
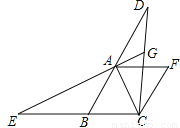
如图,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,EA,延长EA交CD于点G.
(1)求证:△ACE≌△CBD;
(2)求∠CGE的度数.
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源:北师大版数学九年级上册第二章第三节《用公式法求解一元一次方程》课时练习 题型:填空题
方程x2-3x+1=0的解是__________
【解析】观察原方程,可用公式法求解;首先确定a、b、c的值,在b2-4ac≥0的前提条件下,代入求根公式进行计算. 【解析】 a=1,b=-3,c=1, b2-4ac=9-4=5>0, x=; ∴x1=,x2=.查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级上册第一章特殊平行四边形第二节《矩形的性质与判定》课时练习 题型:单选题
如图,矩形的两条对角线的一个交角为60°,两条对角线的长度的和为20cm,则这个矩形的一条较短边的长度为( )
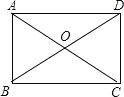
A. 10cm B. 8cm C. 6cm D. 5cm
D 【解析】试题解析:∵四边形ABCD是矩形, ∴OA=OC=AC,OD=OB=BD,AC=BD, ∴OA=OB, ∵AC+BD=20, ∴AC=BD=10cm, ∴OA=OB=5cm, ∵OA=OB,∠AOB=60°, ∴△OAB是等边三角形, ∴AB=OA=5cm, 故选D.查看答案和解析>>
科目:初中数学 来源:北师大版九年级数学(上)第二章《一元二次方程》同步测试:2.4用因式分解法求解一元二次方程 题型:填空题
一元二次方程x(x-2)=0的解是______.
x1=0,x2=2. 【解析】试题解析: , 或, . 故答案为:查看答案和解析>>
科目:初中数学 来源:北师大版九年级数学(上)第二章《一元二次方程》同步测试:2.4用因式分解法求解一元二次方程 题型:单选题
若(a2+b2)(a2+b2-2)=8,则a2+b2的值为( )
A. 4或-2 B. 4 C. -2 D. -4
B 【解析】【解析】 ,∴,∴或(舍去),∴.故选B.查看答案和解析>>
科目:初中数学 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:填空题
如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是______.
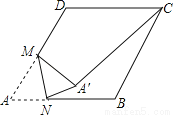
查看答案和解析>>
科目:初中数学 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:单选题
菱形的两条对角线长分别为9cm与4cm,则此菱形的面积为( )cm2.
A. 12 B. 18 C. 20 D. 36
B 【解析】试题分析:根据对角线的长可以求得菱形的面积, 根据S=ab=×4cm×9cm=18cm2, 故选B.查看答案和解析>>
科目:初中数学 来源:广西柳州市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
有理数m,n在数轴上分别对应的点为M,N,则下列式子结果为负数的个数是( )
①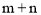 ;②
;②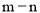 ;③
;③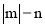 ;④
;④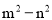 ;⑤
;⑤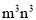 .
.
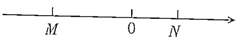
A. 2个 B. 3个 C. 4个 D. 5个
B 【解析】【解析】 ∵m<0<n,而且|m|>|n|,∴m+n<0,∴①的结果为负数; ∵m<0<n,∴m﹣n<0,∴②的结果为负数; ∵m<0<n,而且|m|>|n|,∴|m|﹣n>0,∴③的结果为正数; ∵m<0<n,而且|m|>|n|,∴m2﹣n2>0,∴④的结果为正数; ∵m<0<n,∴m3n3<0,∴④的结果为负数,∴式子结果为负数的个数是3个:①、②、...查看答案和解析>>
科目:初中数学 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:解答题
小美有红色、白色、蓝色上衣各一件,黄色、黑色长裤各一条.(1)请用画树状图或列表的方法分析小美上衣和长裤有多少种不同的搭配情况;(2)其中小美穿蓝色上衣的概率是多少?
(1)小美上衣和长裤有6种不同的搭配情况(2) 【解析】试题分析:(1)列出表格即可得小美上衣和长裤不同搭配的所有情况.(2)利用概率公式直接求解即可. 试题解析:(1)列表得, 红色 白色 蓝色 黄色 (红色,黄色) (白色,黄色) (蓝色,黄色) 黑色 (红色,黑色) ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com