
С���к�ɫ����ɫ����ɫ���¸�һ������ɫ����ɫ�����һ������1�����û���״ͼ���б��ķ�������С�����ºͳ����ж����ֲ�ͬ�Ĵ����������2������С������ɫ���µĸ����Ƕ���?
��1��С�����ºͳ�����6�ֲ�ͬ�Ĵ��������2�� �������������������1���г����ɵ�С�����ºͳ��㲻ͬ����������������2�����ø��ʹ�ʽֱ����⼴�ɣ� �����������1���б��ã� ��ɫ ��ɫ ��ɫ ��ɫ ����ɫ����ɫ�� ����ɫ����ɫ�� ����ɫ����ɫ�� ��ɫ ����ɫ����ɫ�� ... �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��������ѧ��һѧ��1.1.1���εĶ��������� ͬ����ϰ ���ͣ������
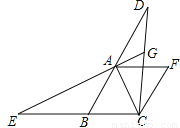
��ͼ��������ABCF�У���ABC=60�㣬�ӳ�BA����D���ӳ�CB����E��ʹBE=AD������CD��EA���ӳ�EA��CD�ڵ�G��
��1����֤����ACE�ա�CBD��
��2�����CGE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ�����������2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
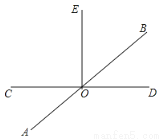
��ͼ����ֱ֪��AB��CD�ཻ�ڵ�O���ڡ�COB���ڲ�������OE.
��1������AOC=36�㣬��COE=90�㣬���BOE�Ķ�����
��2������COE����EOB����BOD=4��3��2�����AOE�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ�����������2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
���б����У�����ȷ���ǣ� ��
A. 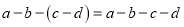 B.
B. 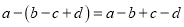
C. 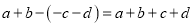 D.
D. 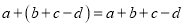
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ˮ��2018����꼶��ѧ����ĩģ�Ŀ�����ѧ�Ծ� ���ͣ������
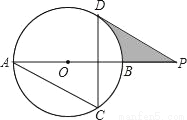
��ͼ��ABΪ��O��ֱ����AC��DCΪ�ң���ACD=60�㣬PΪAB�ӳ����ϵĵ㣬��APD=30�㣮
��1����֤��DP�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ3cm����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ˮ��2018����꼶��ѧ����ĩģ�Ŀ�����ѧ�Ծ� ���ͣ������
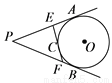
��ͼ��PA��PB�ֱ����O�����ڵ�A��B����O������EF�ֱ�PA��PB�ڵ�E��F���е�C���ϣ���PA��Ϊ2�����PEF���ܳ���__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ˮ��2018����꼶��ѧ����ĩģ�Ŀ�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ���Ҳ��ŵ����Ŵ����ĸ߶ȷֱ���AB=8�ף�CD=12�ף�������ˮƽ����BD=5�ף�һ�۲��ߵ��۾���EF=1.6�ף���E��B��D��һ��ֱ���ϣ����۲��ߵ�����FACǡ�þ����������Ķ���ʱ���ı���ABDC�������ǹ۲��ߵ�ä�������ʱ�۲�������AB�ľ���EB���ڣ�������
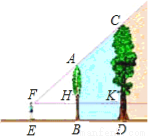
A��8�� B��7�� C��6�� D��5��
A �������� ����FH=x����FK=FH+FK=x+5���ٸ���AH��CD���ɵó���AFH�ס�CFK�������������εĶ�Ӧ�߳ɱ����������x��ֵ�������ó�EB�ij��� �������� ��AB=8�ף�CD=12�ף�������ˮƽ����BD=5�ף�һ�۲��ߵ��۾���EF=1.6�ף� ��EB=FH��BD=HK=5�ף�HB=KD=EF=1.6�ף� ��FH=x����FK=FH+FK=x+5��AH=...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ��������Ϫ��2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ����ABC�У�AB=AC��BC=24��cosB=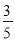 .
.
��1��AB�ij�����2����ABC�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�γ���2016-2017ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ƽ��ֱ������ϵ�У�����A��a����b���ڵ�һ�����ڣ����B��a��b�����ڵ������ǣ�������
A. ��һ���� B. �ڶ����� C. �������� D. ��������
D ���������ߵ�A(a��?b)�ڵ�һ�����ڣ� ��a>0��?b>0�� ��b<0�� ���B(a��b)���ڵ������ǵ������ޡ� ��ѡD.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com