
方程x2﹣4x+5=0根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 有一个实数根 D. 没有实数根
D 【解析】试题分析: ∵a=1,b=﹣4,c=5, ∴△=b2﹣4ac=(﹣4)2﹣4×1×5=﹣4<0, 所以原方程没有实数根.科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
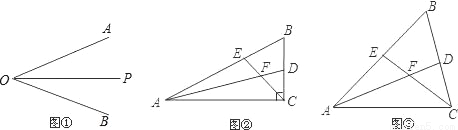
如图①,OP是∠AOB的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;
(2)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:单选题
如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0).下列结论:①ab<0;②b2>4a;③0<a+b+c<2;④0<b<1;⑤当x>-1时,y>0.其中正确结论的个数是( )
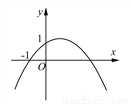
A. 5个 B. 4个 C. 3个 D. 2个
B 【解析】由抛物线的对称轴x=-在y轴右侧,可以判定a、b异号,由此确定①正确; 由抛物线与x轴有两个交点得到b2-4ac>0,又抛物线过点(0,1),得出c=1,由此判定②正确; 由a-b+c=0,及b>0得出a+b+c=2b>0;由b<1,c=1,a<0,得出a+b+c<a+1+1<2,由此判定③正确; 由抛物线过点(-1,0),得出a-b+c=0,即a=b-1,由a<0得出...查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷 题型:解答题
甲地到乙地的铁路全程总长为1000千米,开通高铁前乘火车从甲地到乙地的时间比开通高铁后从甲地到乙地的时间多4个小时,高铁的速度是普通列车速度的2倍,求高铁的速度.
高铁的速度为250千米/时. 【解析】试题分析: 设普通列车的速度为千米/小时,则高铁的速度是千米/小时,由此可知行驶完全程,普通列车需小时,高铁需小时,根据“开通高铁前乘火车从甲地到乙地的时间比开通高铁后从甲地到乙地的时间多4个小时”即可列出方程,解方程即可求得相应的答案. 试题解析: 【解析】 设普通列车速度为千米/时,则高铁的速度为是千米/小时, 根据题意得:...查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷 题型:填空题
不等式2x﹣10≤0的解集为_____.
x≤5 【解析】解不等式,移项得: ,系数化为1得: . ∴不等式的解集为.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市七年级数学科期末检测模拟 题型:解答题
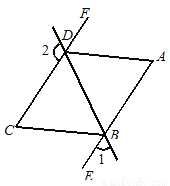
如图12,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与CF平行吗?请说明理由;
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
【解析】
(1)AE∥CF,理由如下:
∵ ∠CDB+∠2=180°, ( 平角的定义 )
∠1+∠2=180°, ( 已知 )
∴ ∠1=∠ , ( )
∴ AE∥CF. ( )
(2)AD与BC的位置关系是: .
∵ AE∥CF,( 已知 )
∴ ∠C=∠ .( )
又∵ ∠A=∠C,( 已知 )
∴ ∠A=∠CBE . ( )
∴ ∥ .( )
(3)
(1)AE∥CF, (2)AD与BC的位置关系是:AD∥BC(3)BC平分∠DBE, 【解析】试题分析:(1)证明∠1=∠ CDB ,利用同位角相等,两直线平行即可证得; (2)根据平行线的性质可得∠A=∠CBE,然后利用平行线的判定方法即可证得; (3)根据平行线的性质即可得∠EBC=∠CBD,由DA平分∠BDF可得∠ADB=∠BDF,再由等量代换得 ∠CBD=∠DBE,从而结论得...查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市七年级数学科期末检测模拟 题型:填空题
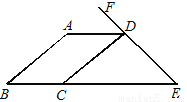
如图8,已知AB∥CD,AD∥ BE,∠B=40°,∠E=48°,则∠CDF=_______度.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017年中考数学二模试卷 题型:解答题
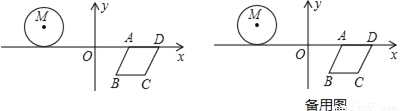
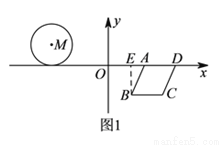
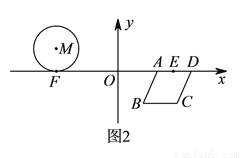
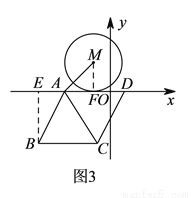
如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(﹣3,1),点A的坐标为(2,0),点B的坐标为(1,﹣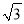 ),点D在x轴上,且点D在点A的右侧.
),点D在x轴上,且点D在点A的右侧.
(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒2个单位长度的速度平移,菱形ABCD沿x轴向左以每秒3个单位长度的速度平移,设菱形移动的时间为t(秒),当⊙M与AD相切,且切点为AD的中点时,连接AC,求t的值及∠MAC的度数;
(3)在(2)的条件下,当点M与AC所在的直线的距离为1时,求t的值.
【答案】(1)菱形的周长为8;(2)t=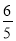 ,∠MAC=105°;(3)当t=1﹣
,∠MAC=105°;(3)当t=1﹣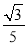 或t=1+
或t=1+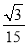 时,圆M与AC相切.
时,圆M与AC相切.
【解析】试题分析:(1)过点B作BE⊥AD,垂足为E.由点A和点B的坐标可知:BE=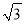 ,AE=1,依据勾股定理可求得AB的长,从而可求得菱形的周长;(2)记 M与x轴的切线为F,AD的中点为E.先求得EF的长,然后根据路程=时间×速度列出方程即可;平移的图形如图3所示:过点B作BE⊥AD,垂足为E,连接MF,F为 M与AD的切点.由特殊锐角三角函数值可求得∠EAB=60°,依据菱形的性质可得到∠FAC=60°,然后证明△AFM是等腰直角三角形,从而可得到∠MAF的度数,故此可求得∠MAC的度数;(3)如图4所示:连接AM,过点作MN⊥AC,垂足为N,作ME⊥AD,垂足为E.先求得∠MAE=30°,依据特殊锐角三角函数值可得到AE的长,然后依据3t+2t=5-AE可求得t的值;如图5所示:连接AM,过点作MN⊥AC,垂足为N,作ME⊥AD,垂足为E.依据菱形的性质和切线长定理可求得∠MAE=60°,然后依据特殊锐角三角函数值可得到EA=
,AE=1,依据勾股定理可求得AB的长,从而可求得菱形的周长;(2)记 M与x轴的切线为F,AD的中点为E.先求得EF的长,然后根据路程=时间×速度列出方程即可;平移的图形如图3所示:过点B作BE⊥AD,垂足为E,连接MF,F为 M与AD的切点.由特殊锐角三角函数值可求得∠EAB=60°,依据菱形的性质可得到∠FAC=60°,然后证明△AFM是等腰直角三角形,从而可得到∠MAF的度数,故此可求得∠MAC的度数;(3)如图4所示:连接AM,过点作MN⊥AC,垂足为N,作ME⊥AD,垂足为E.先求得∠MAE=30°,依据特殊锐角三角函数值可得到AE的长,然后依据3t+2t=5-AE可求得t的值;如图5所示:连接AM,过点作MN⊥AC,垂足为N,作ME⊥AD,垂足为E.依据菱形的性质和切线长定理可求得∠MAE=60°,然后依据特殊锐角三角函数值可得到EA=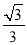 ,最后依据3t+2t=5+AE.列方程求解即可.
,最后依据3t+2t=5+AE.列方程求解即可.
试题解析:( 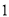 )如图1所示:过点
)如图1所示:过点 作
作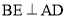 ,垂足为
,垂足为 ,
,
∵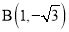 ,
, 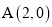 ,
,
∴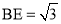 ,
, 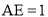 ,
,
∴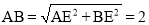 ,
,
∵四边形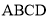 为菱形,
为菱形,
∴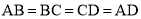 ,
,
∴菱形的周长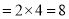 .
.
(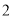 )如图2所示,⊙
)如图2所示,⊙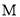 与
与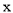 轴的切线为
轴的切线为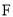 ,
,  中点为
中点为 ,
,
∵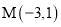 ,
,
∴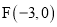 ,
,
∵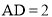 ,且
,且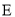 为
为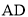 中点,
中点,
∴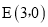 ,
, 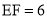 ,
,
∴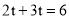 ,
,
解得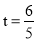 .
.
平移的图形如图3所示:过点 作
作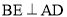 ,
,
垂足为 ,连接
,连接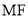 ,
, 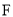 为⊙
为⊙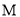 与
与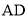 切点,
切点,
∵由(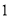 )可知,
)可知, 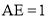 ,
, 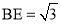 ,
,
∴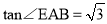 ,
,
∴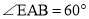 ,
,
∴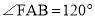 ,
,
∵四边形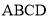 是菱形,
是菱形,
∴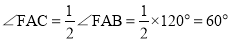 ,
,
∵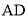 为
为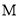 切线,
切线,
∴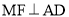 ,
,
∵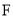 为
为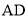 的中点,
的中点,
∴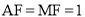 ,
,
∴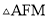 是等腰直角三角形,
是等腰直角三角形,
∴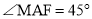 ,
,
∴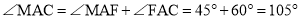 .
.
(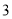 )如图4所示:连接
)如图4所示:连接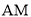 ,过点作
,过点作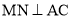 ,垂足为
,垂足为 ,作
,作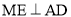 ,垂足为
,垂足为 ,
,
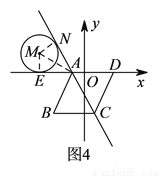
∵四边形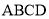 为菱形,
为菱形, 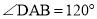 ,
,
∴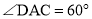 .
.
∵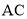 、
、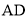 是圆
是圆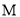 的切线
的切线
∴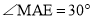 ,
,
∵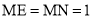 。
。
∴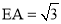 ,
,
∴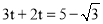 ,
,
∴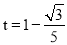 .
.
如图5所示:连接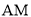 ,过点作
,过点作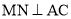 ,垂足为
,垂足为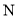 ,作
,作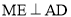 ,垂足为
,垂足为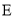 ,
,
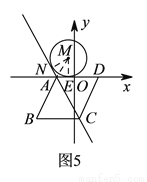
∵四边形 为菱形,
为菱形, 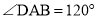 ,
,
∴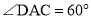 ,
,
∴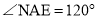 ,
,
∵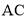 、
、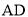 是圆
是圆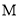 的切线,
的切线,
∴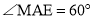 ,
,
∵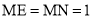 ,
,
∴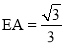 ,
,
∴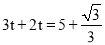 ,
,
∴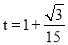 .
.
综上所述,当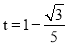 或
或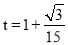 时,圆
时,圆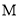 与
与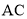 相切.
相切.
点睛:此题是一道圆的综合题.圆中的方法规律总结:1、分类讨论思想:研究点、直线和圆的位置关系时,就要从不同的位置关系去考虑,即要全面揭示点、直线和元的各种可能的位置关系.这种位置关系的考虑与分析要用到分类讨论思想.1、转化思想:(1)化“曲面”为“平面”(2)化不规则图形面积为规则图形的面积求解.3、方程思想:再与圆有关的计算题中,除了直接运用公式进行计算外,有时根据图形的特点,列方程解答,思路清楚,过程简捷.
【题型】解答题
【结束】
28
如图1,在平面直角坐标系中,直线l与x轴、y轴分别交于点B(4,0)、C(0,3),点A为x轴负半轴上一点,AM⊥BC于点M交y轴于点N(0, 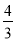 ).已知抛物线y=ax2+bx+c经过点A,B,C.
).已知抛物线y=ax2+bx+c经过点A,B,C.
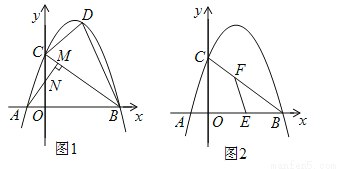
(1)求抛物线的函数式;
(2)连接AC,点D在线段BC上方的抛物线上,连接DC,DB,若△BCD和△ABC面积满足S△BCD= 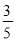 S△ABC, 求点D的坐标;
S△ABC, 求点D的坐标;
(3)如图2,E为OB中点,设F为线段BC上一点(不含端点),连接EF.一动点P从E出发,沿线段EF以每秒3个单位的速度运动到F,再沿着线段PC以每秒5个单位的速度运动到C后停止.若点P在整个运动过程中用时最少,请直接写出最少时间和此时点F的坐标.
(1)y=﹣x2+x+3(2)D点坐标为(1, )或(3,3)(3)点P在整个运动过程中所用的最少时间2××2=3秒,此时点F的坐标为(2, ) 【解析】试题分析:(1)根据点N(0, ),得到ON=,再证明△AON∽△COB,利用相似比计算出OA=1,得到A(-1,0),然后利用交点式可求出抛物线解析式为y=-x2+x+3; (2)先利用待定系数法求出直线BC的解析式为y=-x+3,...查看答案和解析>>
科目:初中数学 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:填空题
已知一元二次方程x2﹣3x﹣2=0的两个实数根为x1,x2,则(x1﹣1)(x2﹣1)的值是_____.
-4 【解析】∵一元二次方程x2﹣3x﹣2=0的两个实数根为x1,x2, ∴x1+x2=3,x1x2=-2, ∴(x1-1)(x2-1)=x1x2-x2-x1+1=x1x2-(x1+x2)+1=-2-3+1=-4, 故答案为:-4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com