
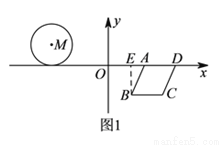
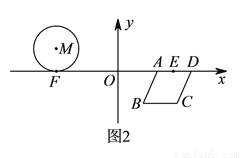
��ͼ����M������ABCD��ƽ��ֱ������ϵ�У���M������Ϊ����3��1������A������Ϊ��2��0������B������Ϊ��1����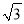 ������D��x���ϣ��ҵ�D�ڵ�A���Ҳ࣮
������D��x���ϣ��ҵ�D�ڵ�A���Ҳ࣮
��1��������ABCD���ܳ���
��2������M��x��������ÿ��2����λ���ȵ��ٶ�ƽ�ƣ�����ABCD��x��������ÿ��3����λ���ȵ��ٶ�ƽ�ƣ��������ƶ���ʱ��Ϊt���룩������M��AD���У����е�ΪAD���е�ʱ������AC����t��ֵ����MAC�Ķ�����
��3���ڣ�2���������£�����M��AC���ڵ�ֱ�ߵľ���Ϊ1ʱ����t��ֵ��
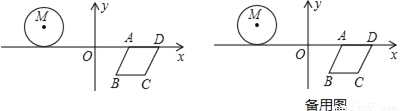
���𰸡���1�����ε��ܳ�Ϊ8����2��t=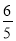 ����MAC=105�㣻��3����t=1��
����MAC=105�㣻��3����t=1��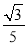 ��t=1+
��t=1+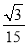 ʱ��ԲM��AC���У�
ʱ��ԲM��AC���У�
�������������������1������B��BE��AD������ΪE���ɵ�A�͵�B�������֪��BE=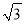 ��AE=1�����ݹ��ɶ��������AB�ij����Ӷ���������ε��ܳ�����2���� M��x�������ΪF��AD���е�ΪE�������EF�ij���Ȼ�����·��=ʱ����ٶ��г����̼��ɣ�ƽ�Ƶ�ͼ����ͼ3��ʾ������B��BE��AD������ΪE������MF��FΪ M��AD���е㣮������������Ǻ���ֵ����á�EAB=60�㣬�������ε����ʿɵõ���FAC=60�㣬Ȼ��֤����AFM�ǵ���ֱ�������Σ��Ӷ��ɵõ���MAF�Ķ������ʴ˿���á�MAC�Ķ�������3����ͼ4��ʾ������AM��������MN��AC������ΪN����ME��AD������ΪE������á�MAE=30�㣬��������������Ǻ���ֵ�ɵõ�AE�ij���Ȼ������3t+2t=5-AE�����t��ֵ����ͼ5��ʾ������AM��������MN��AC������ΪN����ME��AD������ΪE���������ε����ʺ����߳���������á�MAE=60�㣬Ȼ����������������Ǻ���ֵ�ɵõ�EA=
��AE=1�����ݹ��ɶ��������AB�ij����Ӷ���������ε��ܳ�����2���� M��x�������ΪF��AD���е�ΪE�������EF�ij���Ȼ�����·��=ʱ����ٶ��г����̼��ɣ�ƽ�Ƶ�ͼ����ͼ3��ʾ������B��BE��AD������ΪE������MF��FΪ M��AD���е㣮������������Ǻ���ֵ����á�EAB=60�㣬�������ε����ʿɵõ���FAC=60�㣬Ȼ��֤����AFM�ǵ���ֱ�������Σ��Ӷ��ɵõ���MAF�Ķ������ʴ˿���á�MAC�Ķ�������3����ͼ4��ʾ������AM��������MN��AC������ΪN����ME��AD������ΪE������á�MAE=30�㣬��������������Ǻ���ֵ�ɵõ�AE�ij���Ȼ������3t+2t=5-AE�����t��ֵ����ͼ5��ʾ������AM��������MN��AC������ΪN����ME��AD������ΪE���������ε����ʺ����߳���������á�MAE=60�㣬Ȼ����������������Ǻ���ֵ�ɵõ�EA=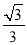 ���������3t+2t=5+AE���з�����⼴�ɣ�
���������3t+2t=5+AE���з�����⼴�ɣ�
����������� 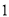 ����ͼ1��ʾ������
����ͼ1��ʾ������ ��
��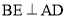 ������Ϊ
������Ϊ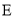 ��
��
��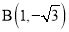 ��
�� 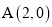 ��
��
��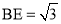 ��
�� 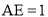 ��
��
��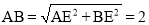 ��
��
���ı���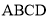 Ϊ���Σ�
����
��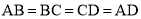 ��
��
�����ε��ܳ�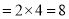 ��
��
��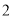 ����ͼ2��ʾ����
����ͼ2��ʾ����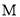 ��
��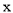 �������Ϊ
�������Ϊ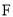 ��
�� 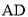 �е�Ϊ
�е�Ϊ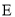 ��
��
��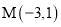 ��
��
��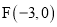 ��
��
��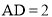 ����
����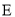 Ϊ
Ϊ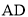 �е㣬
�е㣬
��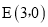 ��
�� 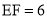 ��
��
��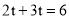 ��
��
���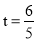 ��
��
ƽ�Ƶ�ͼ����ͼ3��ʾ������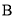 ��
��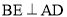 ��
��
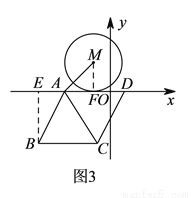
����Ϊ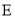 ������
������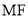 ��
�� 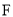 ��
��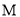 ��
��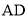 �е㣬
�е㣬
���ɣ�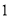 ����֪��
����֪�� 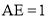 ��
�� 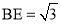 ��
��
��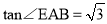 ��
��
��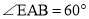 ��
��
��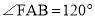 ��
��
���ı���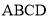 �����Σ�
������
��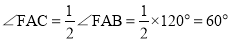 ��
��
��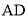 Ϊ
Ϊ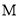 ���ߣ�
���ߣ�
��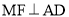 ��
��
��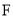 Ϊ
Ϊ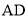 ���е㣬
���е㣬
��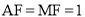 ��
��
��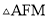 �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
��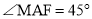 ��
��
��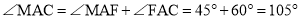 ��
��
��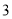 ����ͼ4��ʾ������
����ͼ4��ʾ������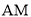 ��������
��������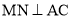 ������Ϊ
������Ϊ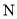 ����
����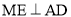 ������Ϊ
������Ϊ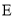 ��
��
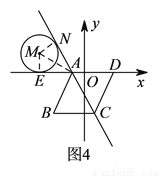
���ı���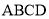 Ϊ���Σ�
���� 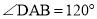 ��
��
��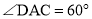 ��
��
��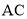 ��
��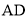 ��Բ
��Բ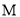 ������
������
��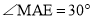 ��
��
��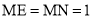 ��
��
��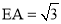 ��
��
��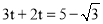 ��
��
��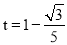 ��
��
��ͼ5��ʾ������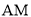 ��������
��������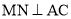 ������Ϊ
������Ϊ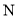 ����
����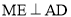 ������Ϊ
������Ϊ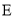 ��
��
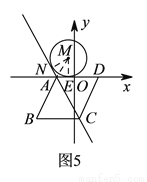
���ı��� Ϊ���Σ�
���� 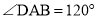 ��
��
��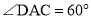 ��
��
��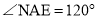 ��
��
��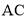 ��
��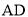 ��Բ
��Բ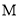 �����ߣ�
�����ߣ�
��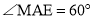 ��
��
��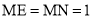 ��
��
��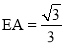 ��
��
��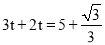 ��
��
��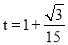 ��
��
������������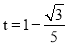 ��
��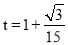 ʱ��Բ
ʱ��Բ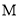 ��
��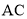 ����
����
�㾦��������һ��Բ���ۺ���.Բ�еķ��������ܽ1����������˼�룺�о��㡢ֱ�ߺ�Բ��λ�ù�ϵʱ����Ҫ�Ӳ�ͬ��λ�ù�ϵȥ���ǣ���Ҫȫ���ʾ�㡢ֱ�ߺ�Ԫ�ĸ��ֿ��ܵ�λ�ù�ϵ.����λ�ù�ϵ�Ŀ��������Ҫ�õ���������˼��.1��ת��˼�룺��1���������桱Ϊ��ƽ�桱��2����������ͼ�����Ϊ����ͼ�ε�������.3������˼�룺����Բ�йصļ������У�����ֱ�����ù�ʽ���м����⣬��ʱ����ͼ�ε��ص㣬�з��̽��˼·��������̼��.
�����͡������
��������
28
��ͼ1����ƽ��ֱ������ϵ�У�ֱ��l��x�ᡢy��ֱ��ڵ�B��4��0����C��0��3������AΪx�Ḻ������һ�㣬AM��BC�ڵ�M��y���ڵ�N��0�� 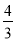 ������֪������y=ax2+bx+c������A��B��C��
������֪������y=ax2+bx+c������A��B��C��
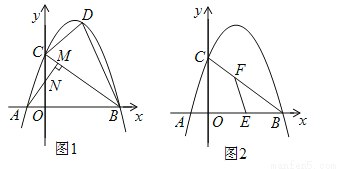
��1���������ߵĺ���ʽ��
��2������AC����D���߶�BC�Ϸ����������ϣ�����DC��DB������BCD�͡�ABC�������S��BCD= 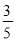 S��ABC�� ���D�����ꣻ
S��ABC�� ���D�����ꣻ
��3����ͼ2��EΪOB�е㣬��FΪ�߶�BC��һ�㣨�����˵㣩������EF��һ����P��E���������߶�EF��ÿ��3����λ���ٶ��˶���F���������߶�PC��ÿ��5����λ���ٶ��˶���C��ֹͣ������P�������˶���������ʱ���٣���ֱ��д������ʱ��ʹ�ʱ��F�����꣮
��1��y=��x2+x+3��2��D������Ϊ��1�� ����3��3����3����P�������˶����������õ�����ʱ��2����2=3�룬��ʱ��F������Ϊ��2�� �� �������������������1�����ݵ�N��0�� �����õ�ON=����֤����AON�ס�COB���������Ʊȼ����OA=1���õ�A��-1��0����Ȼ�����ý���ʽ����������߽���ʽΪy=-x2+x+3�� ��2�������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=-x+3��... ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�����2018����꼶��ѧ�ϲ���ĩ���Ծ� ���ͣ������
����װ�д�С��ͬ��2�������2������
��1���ȴӴ�������1�����Żأ���Ͼ��Ⱥ�������1����
�����һ���������ڶ�����������ĸ��ʣ�
��������������������1�������1������ĸ��ʣ�
��2���ȴӴ�������1����Żأ�������1����������������������1�������1������ĸ����Ƕ��٣���ֱ��д�������
��1���٣��ڣ���2��. �������������������1�������ȸ������⻭����״ͼ���б���Ȼ����ͼ��������еȿ��ܵĽ�����һ���������ڶ����������������������ø��ʹ�ʽ������ô�. �������ɢ��������������������1�������1�����������������ø��ʹ�ʽ������ô�. ��2�����ȴӴ�������1����Żأ�������1�����еȿ��ܵĽ��Ϊ��4��3=12���֣���������������������1������...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꼪��ʡ�������п���ѧģ���Ծ� ���ͣ���ѡ��
����x2��4x+5=0��������ǣ�������
A. ����������ȵ�ʵ���� B. ��������ȵ�ʵ����
C. ��һ��ʵ���� D. û��ʵ����
D ����������������� ��a=1��b=��4��c=5�� ���=b2��4ac=����4��2��4��1��5=��4��0�� ����ԭ����û��ʵ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��ȵ�һѧ�ں���ʡ���������꼶��ѧ����ĩ���ģ�� ���ͣ���ѡ��
��ͼ��ֱ��AB,CD���ڵ�O��OEƽ�֡�AOD������COE=108�㣬���1���ڣ� ��
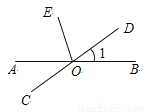
A. 30º B. 36º C. 48º D. 72º
B ���������ߡ�COE=108�㣬 ���DOE=180��-108��=72��. ��OEƽ�֡�AOD�� ���AOD=2��DOE=2��72��=144��, ���BOD=180��-144��=36��. ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��ȵ�һѧ�ں���ʡ���������꼶��ѧ����ĩ���ģ�� ���ͣ���ѡ��
��m=-3ʱ������ʽm2-2m+1��ֵ�ǣ� ��
A. -11 B. 1 C. 4 D. 16
D ����������m=-3 ��m2-2m+1=(-3)2-2��(-3)+1=9+6+1=16. ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017���п���ѧ��ģ�Ծ� ���ͣ������
С���μ�ij�����������Ŀ��������������ѡ���˳��ͨ�أ���һ����ѡ����3��ѡ��ڶ�����ѡ����4��ѡ���������С�������ᣬ����С������һ����������û���ã�ʹ�á�������������������ȥ������һ���һ������ѡ���
��1�����С����һ�ⲻʹ�á�����������ôС����Ե�һ����ĸ�����________��
��2�����С���������������ڵڶ���ʹ�ã�������״ͼ�����б�������С��˳��ͨ�صĸ��ʣ�
��1����2�� �������������������1���ɵ�һ����ѡ����3��ѡ�ֱ�����ø��ʹ�ʽ��⼴����ô𰸣���2�����ȷֱ���A��B��C��ʾ��һ����ѡ���3��ѡ�a��b��c��ʾʣ�µĵڶ�����ѡ���3��ѡ�Ȼ��������⻭����״ͼ��������״ͼ������еȿ��ܵĽ����С��˳��ͨ�ص�����������ø��ʹ�ʽ������ô𰸣� �����������1���ߵ�һ����ѡ����3��ѡ� ��С����һ�ⲻʹ�á�������,��ôС��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017���п���ѧ��ģ�Ծ� ���ͣ������
��ͼ����֪�ı���ABCD�Ǿ��Σ��Ѿ�����ֱ��AC�۵�����B���ڵ�E��������DE����DE��AC=3��5����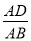 ��ֵΪ________��
��ֵΪ________��
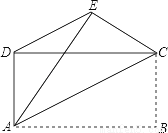
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������2018����꼶����ĩģ����ѧ�Ծ� ���ͣ������
Ϊ�˸���С��������ijС������Ҫ��һ��һ�߿�ǽ��ǽ��25m���Ŀյ�����һ�������̻���ABCD���̻���һ�߿�ǽ�����������ܳ�Ϊ40m��դ��Χס����ͼ���������̻���BC�߳�Ϊxm���̻��������Ϊym2 �� ��y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
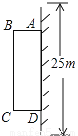
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������2018����꼶��������ѧ�Ծ� ���ͣ���ѡ��
���ڶ��κ���y=2��x��1��2��3��ͼ�����ʣ�����˵������ȷ���ǣ�������
A. �������� B. �Գ���Ϊֱ��x=1 C. ��������Ϊ��1����3�� D. ��СֵΪ3
D �����������ݶ��κ��������ʼ���ֱ���жϣ� �������� A.a=2��0�������������ϣ���������ȷ�� B.�Գ�����x=1����������ȷ�� C.���������ǣ�1����3����������ȷ�� D.��Сֵ�ǩ�3��������� ��ѡD���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com