
如图,在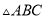 中
中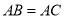 ,点
,点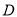 、
、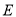 在
在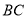 上,连接
上,连接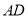 、
、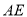 ,如果只添加一个条件使
,如果只添加一个条件使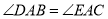 ,则添加的条件不能为( )
,则添加的条件不能为( )

A. 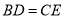 B.
B. 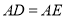 C.
C. 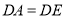 D.
D. 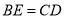
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 第4章 一次函数 单元测试卷 题型:填空题
已知函数y=(k-1)x+k2-1,当k________时,它是一次函数,当k________时,它是正比例函数.
≠1 =-1 【解析】试题解析:∵函数是一次函数, ∴k?1≠0,即k≠1; 函数是正比例函数,则 ∴k=?1. 故答案为:≠1,?1.查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2017-2018学年八年级上学期期中数学 题型:填空题
有一组平行线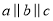 ,过点
,过点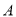 作
作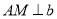 于
于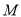 ,作
,作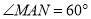 ,且
,且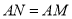 ,过点
,过点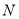 作
作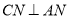 交直线
交直线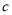 于点
于点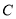 ,在直线
,在直线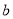 上取点
上取点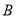 使
使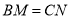 ,则
,则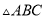 为__________三角形,若直线
为__________三角形,若直线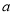 与
与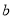 间的距离为
间的距离为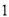 ,
, 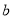 与
与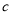 间的距离为
间的距离为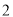 ,则
,则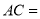 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2017-2018学年八年级上学期期中数学 题型:单选题
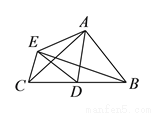
如图, 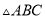 中,
中, 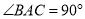 ,
, 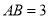 ,
, 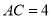 ,点
,点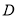 是
是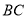 的中点,将
的中点,将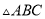 沿
沿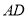 翻折得到
翻折得到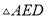 ,连
,连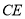 ,则线段
,则线段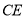 的长等于( )
的长等于( )
A. 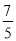 B.
B. 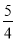 C.
C. 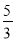 D.
D. 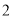
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第三章圆单元检测卷 题型:解答题
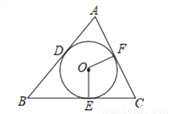
如图,已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,S△ABC=10cm2,C△ABC=10cm且∠C=60°.求:
(1)⊙O的半径r;
(2)扇形OEF的面积(结果保留π);
(3)扇形OEF的周长(结果保留π)
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第三章圆单元检测卷 题型:填空题
直角三角形两直角边为3,4,则其外接圆和内切圆半径之和为________.
3.5 【解析】∵直角三角形两直角边为3,4, ∴斜边长==5, ∴外接圆半径==2.5,内切圆半径==1, ∴外接圆和内切圆半径之和=2.5+1=3.5. 故答案为:3.5.查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:解答题
已知等腰三角形的腰为2 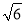 cm,底边为4
cm,底边为4 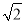 cm,求这个等腰三角形的面积.
cm,求这个等腰三角形的面积.
查看答案和解析>>
科目:初中数学 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
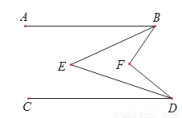
如图,AB∥CD,BE,DE分别平分∠ABF,∠FDC,试问∠E与∠F之间的数量关系如何?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com