
已知,如图ΔABC中,AB=AC,D点在BC上,且BD=AD,DC=AC.并求∠B的度数.

科目:初中数学 来源:2017学年嘉定区第一学期九年级期终学业质量调研测试(2018年初三一模) 题型:单选题
在Rt△ABC中, 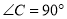 ,
, 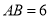 ,
, 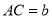 ,下列选项中一定正确的是( )
,下列选项中一定正确的是( )
A. 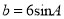 ; B.
; B. 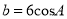 ; C.
; C. 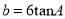 ; D.
; D. 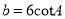 .
.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:单选题
已知三角形三条边分别是1, 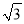 ,2,则该三角形为( )
,2,则该三角形为( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 无法确定
B 【解析】因为 ,根据勾股定理的逆定理可得该三角形为直角三角形,故选B.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:单选题
A、B两地相距36千米,一艘小船从A地匀速顺流航行至B地,又立即从B地匀速逆流返回A地,共用去9小时。已知水流速度为3千米/时,若设该轮船在静水中的速度为x千米/时,则求x时所列方程正确的是( )
A. 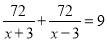 B.
B. 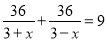
C. 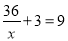 D.
D. 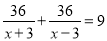
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:单选题
医学研究发现一种新病毒的直径约为0.000043毫米,这个数用科学记数法表为( )
A. 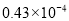 B.
B. 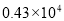 C.
C. 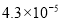 D.
D. 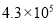
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).
(1)请在图中作出△ABC关于y轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直写出D、E、F的坐标.D、E、F点的坐标是:D( , ) E( , ) F( , );
(2)求四边形ABED的面积.

查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
一个正多边形的每个外角为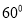 ,则这个正多边形是______边形.
,则这个正多边形是______边形.
查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:填空题
等腰三角形一腰上的高与另一腰所形成的角为50°,则该等腰三角形的顶角为________.
40°或140°. 【解析】当高CD在三角形内部时(如图1),∠ACD=50°,即可求得顶角∠A=40°; 当高CD在三角形外部时(如图2),∠ACD=50°,即可求得顶角∠BAC=∠ACD +∠ADC= 50°+90°=140°. 综上,该等腰三角形的顶角为40°或140°.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:单选题
如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM ≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( )

A. SSS B. SAS C. AAS D. HL
D 【解析】由作法可得OM=ON,PM⊥OM,PN⊥ON, 则∠PMO=∠PNO=90°, 在Rt△PMO和Rt△PNO中, , 所以△POM≌△PON(HL). 故选:D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com