
科目:初中数学 来源:郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型:解答题
计算:
(1)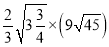
(2)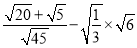 .
.
【答案】(1)45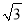 ;(2)1-
;(2)1-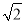
【解析】试题分析:(1)利用二次根式的乘法法则运算
(2)先把各二次根式化简为最简二次根式,然后进行二次根式的除法和乘法运算.
试题解析:
(1)原式 =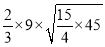 = 45
= 45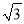 ;
;
(2)原式 =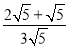 ﹣
﹣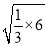 = 1﹣
= 1﹣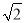 .
.
点睛:此题考查了二次根式的混合运算,熟练掌握运算法则是解题的关键.
【题型】解答题
【结束】
16
已知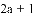
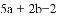
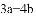
查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:单选题
如果关于x的方程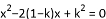 有实数根α、β,那么α+β的取值范围是( )
有实数根α、β,那么α+β的取值范围是( )
A. α+β≥1 B. α+β≤1 C. α+β≥ D. α+β≤
D. α+β≤
查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:解答题
解方程:3x(x﹣2)=2(x﹣2).(因式分解法)
x1=2,x2=. 【解析】移项,得3x(x﹣2)﹣2(x﹣2)=0, 分解因式,得(x﹣2)(3x﹣2)=0, x-2=0,3x-2=0, 解得x1=2,x2=查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:填空题
已知(a2+b2)2﹣(a2+b2)﹣6=0,则a2+b2=___________.
3. 【解析】∵(a²+b²+1)(a²+b²)?6=0, ∴(a²+b²) ²+(a²+b²)?6=0, 设a²+b²=λ,则该方程变为λ²+λ?6=0, 解得:λ=3或?2, 即a²+b²=3或?2(舍去). ∴a²+b²的值为3.查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:填空题
方程x(x-2)=x的根是__________
x1=0,x2=3 【解析】x(x-2) -x=0. x(x-2-1)=0, x (x-3)=0, 所以x1=0,x2=3.查看答案和解析>>
科目:初中数学 来源:江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型:解答题
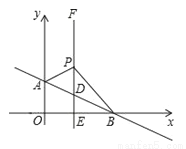
如图,平面直角坐标系中,直线AB: 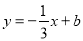 交y轴于点A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).
交y轴于点A(0,1),交x轴于点B.过点E(1,0)作x轴的垂线EF交AB于点D,P是直线EF上一动点,且在点D的上方,设P(1,n).
(1)直线AB的表达式为______;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源:江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型:填空题
将一次函数y=2x的图象向上平移1个单位,所得图象对应的函数表达式为__________.
y=2x+1. 【解析】由“上加下减”的原则可知,将函数y=2x的图象向上平移1个单位所得函数的解析式为y=2x+1, 故答案为:y=2x+1.查看答案和解析>>
科目:初中数学 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
如图,
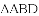
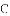
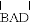 上,且不与点
上,且不与点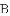
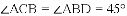
(1)求证: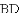
(2)连接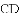
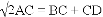 ;
;
(3)若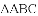
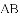
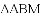
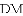
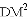 、
、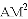 、
、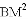 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
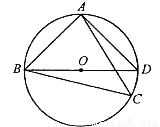
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com