
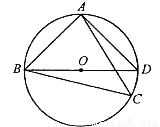
如图,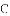
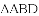
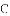
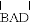 上,且不与点
上,且不与点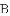
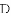
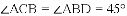
(1)求证: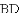
(2)连接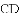
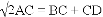 ;
;
(3)若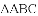
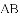
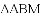
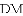
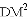 、
、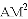 、
、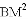 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:填空题
方程x2﹣2x=0的根是______.
x1=0,x2=2. 【解析】∵x(x-2)=0,∴ ,.故答案为:x=0或2.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省中考数学模拟试卷 题型:解答题
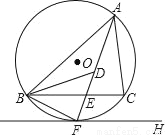
如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连接AF交BC于E,∠ABC的平分线BD交AF于D,连接BF.
(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省中考数学模拟试卷 题型:单选题
如图,直线l1∥l2,AF:FB=2:3,BC:CD=2:1,则AE:EC是( )
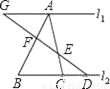
A. 5:2 B. 4:1 C. 2:1 D. 3:2
C 【解析】试题解析:∵AF:FB=2:3,BC:CD=2:1 ∴设AF=2x,BF=3x,BC=2y,CD=y 在△AGF和△BDF中, ∴ ∴AG=2y 在△AGE和△CDE中,AE:EC=AG:CD=2y:y=2:1 故选C.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省中考数学模拟试卷 题型:单选题
下列说法中,正确的是( )
A. 两条对角线相等的四边形是平行四边形
B. 两条对角线相等且互相垂直的四边形是矩形
C. 两条对角线互相垂直平分的四边形是菱形
D. 两条对角线互相垂直平分且相等的四边形是菱形
C 【解析】试题解析:A、两条对角线相等的四边形不一定是平行四边形,如等腰梯形,此选项错误; B、两条对角线相等且互相垂直的四边形不一定是矩形,故此选项错误; C、两条对角线互相垂直平分的四边形是菱形,正确; D、两条对角线互相垂直平分且相等的四边形是正方形,故此选项错误. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
如图,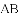
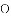
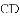
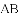
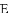
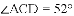
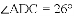
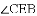
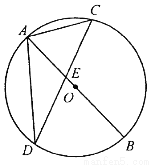
查看答案和解析>>
科目:初中数学 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:填空题
如图,直角坐标系中一条圆弧经过格点A,B,C,其中B点坐标为(3,4),则该弧所在圆心的坐标是_______.
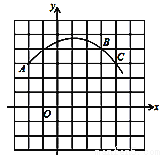
查看答案和解析>>
科目:初中数学 来源:山东省聊城市莘县2017-2018学年八年级(上)期中数学试卷 题型:解答题
化简:
(1)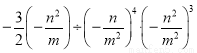
(2)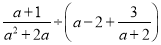
查看答案和解析>>
科目:初中数学 来源:安徽省亳州市利辛县2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
若一个三角形的两边长分别为3和7,且第三边长为整数,则这样的三角形共有( )
A. 2个 B. 3个 C. 4个 D. 5个
D 【解析】设第三边为a,根据三角形的三边关系,得:7-3<a<3+7,即4<a<10,因为a为整数,所以a可取5、6、7、8、9,即符合条件的三角形关于5个,故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com