
科目:初中数学 来源:黄金30题系列 九年级数学 小题易丢分 题型:单选题
因为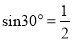 ,
, 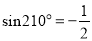 ,所以
,所以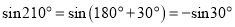 ;因为
;因为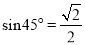 ,
, 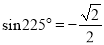 ,所以
,所以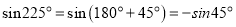 ,由此猜想,推理知:一般地当
,由此猜想,推理知:一般地当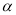 为锐角时有
为锐角时有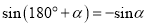 ,由此可知:
,由此可知: 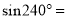 ( ).
( ).
A. 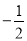 B.
B. 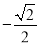 C.
C. 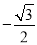 D.
D. 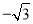
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年七年级(上)期中数学试卷(解析版) 题型:解答题
计算
(1)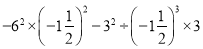
(2)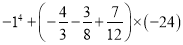
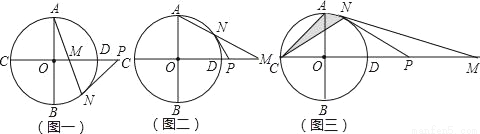
(3)0.5+(﹣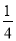 )﹣2.75+(﹣
)﹣2.75+(﹣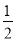 )﹣(﹣3)
)﹣(﹣3)
(4)3(m2n+mn)﹣4(mn﹣2m2n)+mn.
(1)﹣72;(2)26;;(3)0;(4)11m2n 【解析】试题分析: (1)至(3)题首先确定好运算顺序,再按有理数相关运算的运算法则计算即可; (4)先根据去括号法则去掉括号,再合并同类项即可. 试题解析: (1)原式=﹣36×﹣9×()×3 =﹣81+×3 =﹣81+8 =﹣72 (2)原式=﹣1+(32+9﹣14)=26 (3...查看答案和解析>>
科目:初中数学 来源:2017年广东省韶关市南雄市中考数学模拟试卷 题型:解答题
如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:2017年广东省韶关市南雄市中考数学模拟试卷 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017年广东省韶关市南雄市中考数学模拟试卷 题型:单选题
如图,点C在⊙O上,若∠ACB=30°,则∠AOB等于( )
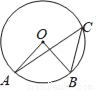
A. 40° B. 60° C. 80° D. 100°
B 【解析】【解析】 ∵∠ACB=30°, ∴∠AOB=2∠ACB=60°. 故选B.查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上期末模拟数学试卷 题型:解答题
综合题。
(1)如图1,在△ABC中,AB=AC,CD⊥AB于D,BE⊥AC于E,试证明:CD=BE.
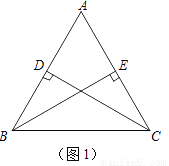
(2)如图2,在△ABC中,仍然有条件“AB=AC,点D,E分别在AB和AC上”.若∠ADC+∠AEB=180°,则CD与BE是否仍相等?若相等,请证明;若不相等,请举反例说明.
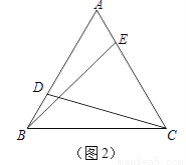
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
下列命题中错误的是( )
A. 矩形的两条对角线相等 B. 等腰梯形的两条对角线互相垂直
C. 平行四边形的两条对角线互相平分 D. 正方形的两条对角线互相垂直且相等
B 【解析】选项A、C、D正确;选项B,等腰梯形的两条对角线相等但不一定垂直,错误.故选B.查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期末测试 题型:填空题
如图,Rt△ABC中,∠ACB=90°,AC=2,BC=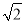 .分别以AB,AC,BC为边,向外作正方形ABDE,正方形ACFG,正方形BCMN,连接GE,DN.则图中阴影部分的总面积是____________.
.分别以AB,AC,BC为边,向外作正方形ABDE,正方形ACFG,正方形BCMN,连接GE,DN.则图中阴影部分的总面积是____________.
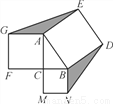
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com