练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列命题中错误的是（　　）

    A. 矩形的两条对角线相等 B. 等腰梯形的两条对角线互相垂直

    C. 平行四边形的两条对角线互相平分 D. 正方形的两条对角线互相垂直且相等

    B 【解析】选项A、C、D正确；选项B，等腰梯形的两条对角线相等但不一定垂直，错误.故选B.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：甘肃省武威市2017-2018学年八年级（上）期中数学试卷 题型：单选题

    已知等腰三角形的两边长分别为3和6，则它的周长等于（　　）

    A. 12 B. 12或15 C. 15 D. 15或18

    C 【解析】试题分析：分两种情况：当3为底时，三角形的三边长为3，6，6，则周长为15； 当3为腰时，三角形的三边长为3，3，6，则不能组成三角形； 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017年广东省韶关市南雄市中考数学模拟试卷 题型：填空题

    若实数a、b满足|a+2|+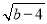=0，则=_________．

    1 【解析】试题分析：根据非负数的性质得： ，解得： ，则原式==1．

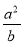    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级上期末模拟数学试卷 题型：解答题

    一个正方体的体积是16cm3，另一正方体的体积是这个正方体体积的4倍，求另一个正方体的表面积．

    96cm2． 【解析】 试题分析：根据题意知大正方体的体积为64cm3，则其棱长为体积的立方根，可求得表面积． 【解析】 根据题意大正方体的体积为16×4=64cm3， 则大正方体的棱长为：=4cm， 故大正方体的表面积为：6×4×4=96cm2．

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级上期末模拟数学试卷 题型：填空题

    如图，在△AOC和△BOC中，若∠AOC=∠BOC，添加一个条件________，使得△AOC≌△BOC．

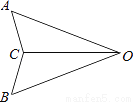
    AO=BO 【解析】添加AO=BO，再加上条件∠AOC=∠BOC，公共边CO=CO，可利用SAS定理判定△AOC≌△BOC．

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级上期末模拟数学试卷 题型：单选题

    为调查某校2000名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机抽取部分学生进行调查，并结合调查数据作出如图所示的扇形统计图．根据统计图提供的信息，可估算出该校喜爱体育节目的学生共有（　　）

    A．300名 B．400名 C．500名 D．600名

    B 【解析】 根据扇形图可以得出该校喜爱体育节目的学生所占比例，进而得出该校喜爱体育节目的学生数目． 【解析】 根据扇形图可得： 该校喜爱体育节目的学生所占比例为：1﹣5%﹣35%﹣30%﹣10%=20%， 故该校喜爱体育节目的学生共有：2000×20%=400， 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型：解答题

    如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点A(-2，2)，B(0，5)，C(0，2).

    (1)将△ABC以点C为旋转中心旋转180°，得到△A1B1C，请画出△A1B1C的图形.

    (2)平移△ABC，使点A的对应点A2坐标为(-2，-6)，请画出平移后对应的△A2B2C2的图形.

    (3)若将△A1B1C绕某一点旋转可得到△A2B2C2，请直接写出旋转中心的坐标.

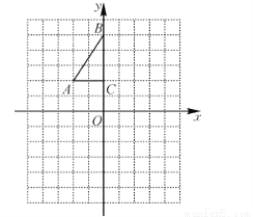
    (1)作图见解析；（2）作图见解析；（3）(0，-2). 【解析】试题分析：（1）利用旋转的性质得出对应点坐标进而得出答案； （2）利用平移规律得出对应点位置，进而得出答案； （3）利用旋转图形的性质，连接对应点，即可得出旋转中心的坐标． 试题解析：（1）如图所示：△A1B1C即为所求； （2）如图所示：△A2B2C2即为所求； （3）旋转中心坐标（0，﹣2）．...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型：单选题

    已知关于x的一元二次方程x2+(2k-3)x+k2=0的两个实数根为x1,x2,且x1+x2 =x1x2,,则k 的值为（ ）

    A. -3 B. 1 C. 1或-3 D. 3

    A 【解析】由根与系数的关系,得x1+x2=?(2k?3)， 因为x1x2=k2,又x1+x2=x1x2， 所以3?2k=k2,即k2+2k?3=0， 解得k=?3或1， 因为△?0时,所以k?34，故k=?3. 故选：A.

    查看答案和解析>>

    科目：初中数学 来源：江西省2017-2018学年度八年级第三次月考数学试卷 题型：填空题

    如图，C、E和B、D、F分别在∠GAH的两边上，且AB=BC=CD=DE=EF，若∠A=18°，则∠GEF的度数是________

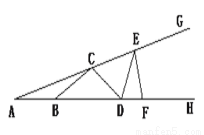
    90°． 【解析】试题分析：∵AB=BC，∴∠ACB=∠A=18°，∴∠CBD=∠A+∠ACB=36°，∵BC=CD，∴∠CDB=∠CBD=36°，∴∠DCE=∠A+∠CDA=18°+36°=54°，∵CD=DE，∴∠CED=∠DCE=54°， ∴∠EDF=∠A+∠AED=18°+54°=72°，∵DE=EF，∴∠EFD=∠EDF=72°， ∴∠GEF=∠A+∠AFE=18°+7...

    查看答案和解析>>

    同步练习册答案