
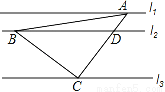
如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A、B、C分别在l1、l2、l3上,AC交l2于D,∠ACB=90°.已知l1与l2的距离为2,l2与l3的距离为6,则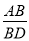 的值为_____.
的值为_____.
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源:2017-2018学年内蒙古乌兰察布市分校九年级(上)期中数学试卷 题型:单选题
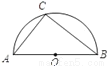
如图,点C是以点O为圆心,AB为直径的半圆上的动点(点C不与点A,B重合),AB=4.设弦AC的长为x,△ABC的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. 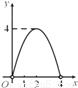 B.
B. 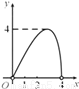 C.
C. 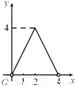 D.
D. 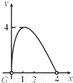
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古包头市七年级(下)期中数学试卷 题型:解答题
如图,在△ABC中,∠A=62°,∠B=74°,∠ACB的平分线交AB于D,DE∥BC交AC于E,求∠EDC的度数.
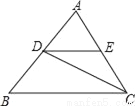
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古包头市七年级(下)期中数学试卷 题型:单选题
如图,描述同位角、内错角、同旁内角关系不正确的是( )
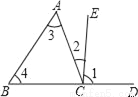
A. ∠1与∠4是同位角 B. ∠2与∠3是内错角
C. ∠3与∠4是同旁内角 D. ∠2与∠4是同旁内角
D 【解析】解:A.∠1与∠4是同位角,故A选项正确; B.∠2与∠3是内错角,故B选项正确; C.∠3与∠4是同旁内角,故C选项正确; D.∠2与∠4是同旁内角,故D选项错误. 故选D.查看答案和解析>>
科目:初中数学 来源:广东省深圳市龙岗区2018届九年级上学期期中考试数学试卷 题型:解答题
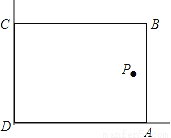
在美化校园的活动中,某综合实践小组的同学借如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形的花圃ABCD(篱笆只围AB、BC两边)设AB=xm.
(1)若想围得花圃面积为192cm2,求x的值;
(2)若在点P处有一棵小树与墙CD、AD的距离分别为15m和6m,要将这棵树围在花圃内(含边界,不考虑树干的粗细),求花圃面积S的最大值.
查看答案和解析>>
科目:初中数学 来源:广东省深圳市龙岗区2018届九年级上学期期中考试数学试卷 题型:单选题
如图,EF过平行四边形ABCD的对角线的交点O,交AD于点E,交BC于点F,已知AB=4,BC=6,OE=3,那么四边形EFCD的周长是( )
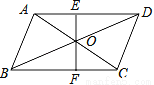
A. 16 B. 13 C. 11 D. 10
A 【解析】根据平行四边形的性质,得 AO=OC,∠EAO=∠FCO,又∠AOE=∠COF, ∴△AOE≌△COF, ∴OF=OE=3,CF=AE, 根据平行四边形的对边相等,得 CD=AB=4,AD=BC=6, 故四边形EFCD的周长=EF+FC+ED+CD=OE+OF+AE+ED+CD=3+3+6+4=16, 故选A.查看答案和解析>>
科目:初中数学 来源:广东省深圳市龙岗区2018届九年级上学期期中考试数学试卷 题型:单选题
下列性质中,矩形具有而菱形不一定具有的是( )
A. 对角线相等 B. 对角线互相平分
C. 对角线互相垂直 D. 邻边相等
A 【解析】菱形的性质有:四边形相等,两组对边分别平行,对角相等,邻角互补,对角线互相垂直且平分,且每一组对角线平分一组对角; 矩形的性质有:两组对边分别相等,两组对边分别平行,四个内角都是直角,对角线相等且平分; ∴矩形具有而菱形不一定具有的性质是对角线相等, 故选A.查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古包头市八年级(下)期中数学试卷 题型:单选题
如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移距离为4,求阴影部分的面积为( )
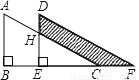
A. 20 B. 24 C. 25 D. 26
D 【解析】由平移的性质知,BE=4,DE=AB=8,可得HE=DE-DH=8-3=5,所以S四边形HDFC=S梯形ABEH=(AB+EH)×BE=(8+5)×4=26.故选D.查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2018届九年级上学期期中考试数学试卷 题型:解答题
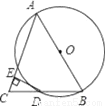
如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com