练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

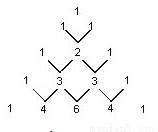
    下面的图表是我国数学家发明的“杨辉三角”，此图揭示了（a+b）n（n为非负整数）的展开式的项数及各项系数的有关规律．请你观察，并根据此规律写出：（a﹣b）5=__________．

    ,

    ,

    ,

    ,

    a5﹣5a4b+10a3b2﹣10a2b3+5ab4﹣b5a5﹣5a4b+10a3b2﹣10a2b3+5ab4﹣b5 【解析】（a﹣b）5=a5﹣5a4b+10a3b2﹣10a2b3+5ab4﹣b5，
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

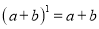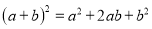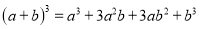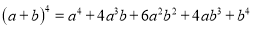    科目：初中数学 来源：2017年湖北省武汉市中考数学模拟试卷二 题型：单选题

    2017的倒数是（　　）

    A. ﹣2017 B. 2017 C. ﹣ D.

    D 【解析】因为积为1的两个数互为倒数，所以2017的倒数是. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：解答题

    已知关于x的一元二次方程x2＋(2m＋1)x＋m2－4＝0.

    (1)当m为何值时，方程有两个不相等的实数根？

    (2)若边长为5的菱形的两条对角线的长分别为方程两根的2倍，求m的值．

    （1）当m＞－时，方程有两个不相等的实数根；（2）m的值为－4. 【解析】试题分析：（1）根据方程的系数结合根的判别式，即可得出解之即可得出结论； （2）设方程的两根分别为 根据根与系数的关系结合菱形的性质，即可得出关于 的一元二次方程，解之即可得出的值，再根据即可确定的值． 试题解析：(1)∵方程有两个不相等的实数根， 解得： ∴当时，方程有两个不相等的实数根. ...

    查看答案和解析>>

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：单选题

    如图，在Rt△ABC中，∠BAC=90°，∠B=60°，△ADE可以由△ABC绕点 A顺时针旋转900得到，点D 与点B是对应点，点E与点C是对应点，连接CE，则∠CED的度数是( )

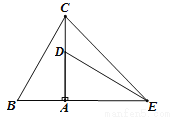
    A. 45° B. 30° C. 25° D. 15°

    D 【解析】试题分析：本题考查了旋转的性质：旋转前后两图形全等，即对应角相等，对应线段相等．也考查了等腰直角三角形的判定与性质．先根据旋转的性质得出AE=AC，∠DAE=∠BAC=90°，那么△CAE为等腰直角三角形，则∠CEA=45°．再根据直角三角形的两个锐角互求出∠BCA=30°，那么∠DEA=∠BCA=30°，那么根据∠CED=∠CEA-∠DEA即可求解． 【解析】 ∵△AD...

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：解答题

    小鹏的家距离学校1600米，一天小鹏从家去上学，出发10分钟后，爸爸发现他的数学课本忘了拿，立即带上课本去追他，在学校门口追上了他，已知爸爸的速度是小鹏速度的2倍，求小鹏的速度．

    小鹏的速度为80米/分． 【解析】试题分析：设小鹏的速度为x米/分，爸爸的速度为2x米/分，根据题意可得，走1600米爸爸比小鹏少用10分钟，据此列方程求解． 【解析】 设小鹏的速度为x米/分，爸爸的速度为2x米/分， 由题意得，﹣=10， 解得：x=80， 经检验，x=80是原分式方程的解，且符合题意． 答：小鹏的速度为80米/分．

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：填空题

    科学家发现一种病毒的直径为0.0043微米，则用科学记数法表示为__________微米．

    4.3×10﹣34.3×10﹣3 【解析】0.0043=4.3×10﹣3．

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：单选题

    下列计算正确的是（ ）

    A. （a3）2=a6 B. a•a2=a2 C. a3+a2=a6 D. （3a）3=9a3

    A 【解析】试题分析：A、根据幂的乘方的定义解答； B、根据同底数幂的乘法解答； C、根据合并同类项法则解答； D、根据积的乘方的定义解答． 【解析】 A、（a3）2=a3×2=a6，故本选项正确； B、a•a2=a1+2=a3，故本选项错误； C、a3和a2不是同类项，不能合并，故本选项错误； D（3a）3=27a3，故本选项错误． 故选A...

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：填空题

    如图，?ABCD的对角线AC、BD相交于点O，点E是BC的中点，若△ABD的周长为8cm，则△BOE的周长是_____cm．

    4 【解析】∵四边形ABCD是平行四边形， ∴BO=DO， ∴O是BD中点， 又∵E是CD中点， ∴OE是△BCD的中位线， ∴OE=BC， 即△DOE的周长=△BCD的周长， ∴△DOE的周长=△DAB的周长。 ∴△DOE的周长=×8=4cm.

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省定安县中考数学仿真试卷（二） 题型：解答题

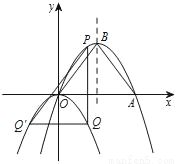
    如图，抛物线y=﹣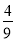x2+bx+c经过原点和点A（6，0），与其对称轴交于点B，P是抛物线y=﹣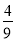x2+bx+c上一动点，且在x轴上方．过点P作x轴的垂线交动抛物线y=﹣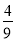（x﹣h）2（h为常数）于点Q，过点Q作PQ的垂线交动抛物线y=﹣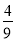（x﹣h）2于点Q′（不与点Q重合），连结PQ′，设点P的横坐标为m．

    （1）求抛物线y=﹣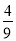x2+bx+c的函数关系式及点B的坐标；

    （2）当h=0时．

    ①求证： ；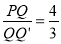

    ②设△PQQ′与△OAB重叠部分图形的周长为l，求l与m之间的函数关系式；

    （3）当h≠0时，是否存在点P，使四边形OAQQ′为菱形？若存在，请直接写出h的值；若不存在，请说明理由．

    （1）y=﹣（x﹣3）2+4，点B的坐标为（3，4）；（2）①证明见解析②l=（3）存在，h=3﹣2或3+2时，四边形OAQQ′为菱形 【解析】试题分析：（1）用待定系数法求得函数解析式，把解析式化为顶点式，直接写出点B的坐标即可；（2）①当h=0时，求得抛物线的解析式，用m表示出点P、Q的坐标，再用m表示出PQ、QQ′的长，计算即可得结论；②分当0＜m≤3时和当3＜m＜6时两种情况求l与m...

    查看答案和解析>>

    同步练习册答案