
已知关于x的一元二次方程x2+(2m+1)x+m2-4=0.
(1)当m为何值时,方程有两个不相等的实数根?
(2)若边长为5的菱形的两条对角线的长分别为方程两根的2倍,求m的值.
(1)当m>-时,方程有两个不相等的实数根;(2)m的值为-4. 【解析】试题分析:(1)根据方程的系数结合根的判别式,即可得出解之即可得出结论; (2)设方程的两根分别为 根据根与系数的关系结合菱形的性质,即可得出关于 的一元二次方程,解之即可得出的值,再根据即可确定的值. 试题解析:(1)∵方程有两个不相等的实数根, 解得: ∴当时,方程有两个不相等的实数根. ... 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源:2016-2017学年内蒙古鄂尔多斯市鄂托克旗八年级(下)期末数学试卷 题型:解答题
计算:(1) 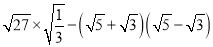
(2)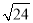 ÷
÷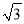 ﹣4×
﹣4×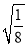 ×(1﹣
×(1﹣ ) 0
) 0
查看答案和解析>>
科目:初中数学 来源:辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型:解答题
列方程解应用题
甲、乙两人同时从相距25千米的A地去B地,甲骑车乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40分钟,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
甲的速度为15千米/小时,乙的速度为5千米/小时. 【解析】试题分析:可设乙的速度为x千米/小时,则甲的速度为3x千米/小时,根据关于路程的等量关系:甲、乙两人行驶的路程和是两个25千米,列出方程求解即可. 【解析】 设乙的速度为x千米/小时,则甲的速度为3x千米/小时,依题意有 3x(3﹣)+3x=25×2, 9x﹣2x+3x=50, 10x=50, x=5...查看答案和解析>>
科目:初中数学 来源:辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型:单选题
如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )

A. 垂线段最短
B. 经过一点有无数条直线
C. 经过两点,有且仅有一条直线
D. 两点之间,线段最短
D 【解析】试题解析:由图可知,剪掉一部分,相当于用一条线段取代了连接原来两点之间的曲线.根据线段公理:两点之间,线段最短,所以剩下树叶的周长比原树叶的周长要小. 故本题应选D.查看答案和解析>>
科目:初中数学 来源:四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型:解答题
.如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,点P在优弧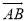 上.
上.
(1)求出A,B两点的坐标;
(2)试确定经过A、B且以点P为顶点的抛物线解析式;
(3)在该抛物线上是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型:填空题
在平面直角坐标系中,二次函数y1=ax2+bx+c(a>0)与一次函数y2=ax+c 的图像交于A、B两点,已知B点的横坐标为2,当y1<y2时,自变量x的取值范围是____.
0查看答案和解析>>
科目:初中数学 来源:四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型:单选题
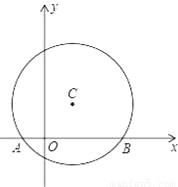
已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac.其中正确的结论的有( )
A. 1个 B. 2个 C. 3个 D. 4个
D 【解析】由题意得: 则: . 得 故①正确;3a+c= <0, 故②错误; 当x=2时, 即4a+2b+c>0 ,故正确; 由于,即2a+b=0,故④正确; 由于函数图像与x轴有两个交点,即b2>4ac,故⑤正确. 综上所述,故选D.查看答案和解析>>
科目:初中数学 来源:北京八十五中2017-2018学年上期期末八年级数学试卷 题型:填空题
下面的图表是我国数学家发明的“杨辉三角”,此图揭示了(a+b)n(n为非负整数)的展开式的项数及各项系数的有关规律.请你观察,并根据此规律写出:(a﹣b)5=__________.
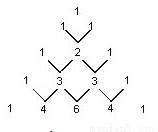
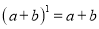 ,
,
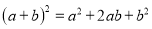 ,
,
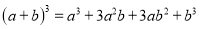 ,
,
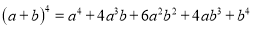 ,
,
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省平凉市中考数学模拟试卷 题型:解答题
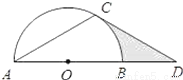
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com