
先化简再求值: 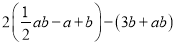 ,其中
,其中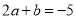 .
.
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源:四川省绵阳市三台县2018届九年级(上)第一学月数学试卷 题型:解答题
阅读下列材料,并用相关的思想方法解决问题.
计算:(1﹣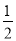 ﹣
﹣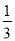 ﹣
﹣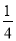 )×(
)×(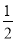 +
+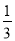 +
+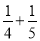 )﹣(1﹣
)﹣(1﹣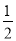 ﹣
﹣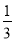 ﹣
﹣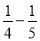 )×(
)×(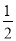 +
+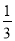 +
+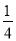 ).
).
令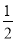 +
+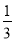 +
+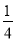 =t,则原式=(1﹣t)(t+
=t,则原式=(1﹣t)(t+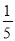 )﹣(1﹣t﹣
)﹣(1﹣t﹣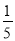 )t=t+
)t=t+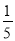 ﹣t2﹣
﹣t2﹣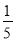 t﹣
t﹣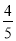 t+t2=
t+t2=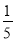 ,
,
问题:
(1)计算:(1﹣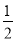 ﹣
﹣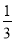 ﹣
﹣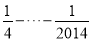 )×(
)×(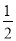 +
+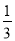 +
+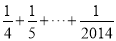 )﹣(1﹣
)﹣(1﹣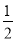 ﹣
﹣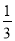 ﹣
﹣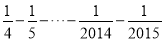 )×(
)×(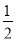 +
+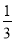 +
+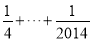 );
);
(2)解方程(x2+5x+1)(x2+5x+7)=7.
(1);(2)方程的解为x=﹣2或﹣3或0或﹣5. 【解析】试题分析:(1)设,则原式= ,进行计算即可; (2)设,则原方程化为: ,求出t的值,再解一元二次方程即可. 试题解析:(1)设, 则原式= = =; (2)设,则原方程化为: ,∴,解得: 或, 当时, , , , ; 当时, , ,△==25﹣4×1×8<0,此时方程无解; ...查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(华师大版):期中检测题 题型:解答题
某地新建了一个企业,每月将生产1 960 t污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号中选择:
污水处理器型号 | A型 | B型 |
处理污水能力(t/月) | 240 | 180 |
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么至少要支付多少钱?
(1)每台A型污水处理器的价格是10万元,每台B型污水处理器的价格是8万元; (2)买6台A型污水处理器、3台B型污水处理器,费用最少,至少要支付84万元钱. 【解析】试题分析:(1)可设每台A型污水处理器的价格是x万元,每台B型污水处理器的价格是y万元,根据等量关系:①2台A型、3台B型污水处理器的总价为44万元,②1台A型、4台B型污水处理器的总价为42万元,列出方程组求解即可; ...查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(华师大版):期中检测题 题型:单选题
已知关于x、y的二元一次方程组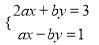 的解为
的解为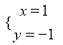 则a-2b的值是( )
则a-2b的值是( )
A. -2 B. 2 C. 3 D. -3
B 【解析】把代入方程组得: , 解得: , 所以a?2b=?2×()=2. 故选:B.查看答案和解析>>
科目:初中数学 来源:内蒙古2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
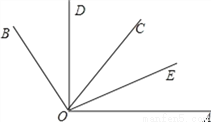
如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.
查看答案和解析>>
科目:初中数学 来源:内蒙古2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
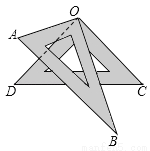
如图,将一副三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,则与∠AOD始终相等的角是 .
查看答案和解析>>
科目:初中数学 来源:内蒙古2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
如图,是正方体的平面展开图,每个面上都标有一个汉字,与“信”字相对的面上的字为( )
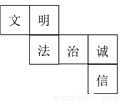
A. 文 B. 明 C. 法 D. 治
B 【解析】【解析】 正方体的表面展开图,相对的面之间一定相隔一个正方形,与“信”字相对的面上的字为“明“.故选B.查看答案和解析>>
科目:初中数学 来源:江苏省南通市2017-2018学年七年级上学期第三次月考数学试卷 题型:解答题
计算:
(1) 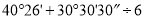 ;
;
(2) 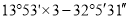 .
.
查看答案和解析>>
科目:初中数学 来源:四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型:解答题
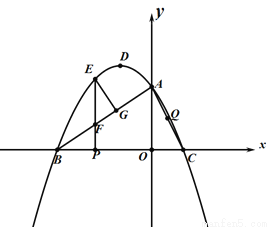
如图,在平面直角坐标系中,抛物线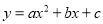 与x轴交于B(-3,0)、C(1,0)两点,与y轴交于点A(0,2),抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.
与x轴交于B(-3,0)、C(1,0)两点,与y轴交于点A(0,2),抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.
(1)求此抛物线的解析式;
(2)过点E作EG⊥AB于点G,Q为线段AC的中点,当△EGF周长最大时,在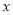 轴上找一点R,使得|RE-RQ|值最大,请求出R点的坐标及|RE-RQ|的最大值;
轴上找一点R,使得|RE-RQ|值最大,请求出R点的坐标及|RE-RQ|的最大值;
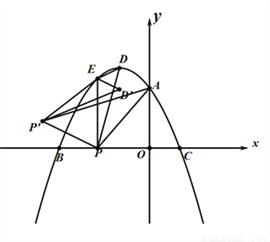
(3)在(2)的条件下,将△PED绕E点旋转得△ED′P′,当△AP′P是以AP为直角边的直角三角形时,求点P′的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com