
如果将抛物线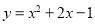 向上平移,使它经过原点,那么所得抛物线的表达式是 .
向上平移,使它经过原点,那么所得抛物线的表达式是 .
科目:初中数学 来源:四川省遂宁市蓬溪县2018届九年级上学期期末考试数学试卷 题型:单选题
等腰梯形的腰长是5cm,中位线的长是4cm,这个等腰梯形的周长是( )
A. 9cm B. 13cm C. 18cm D. 20cm
C 【解析】试题解析:∵等腰梯形ABCD的中位线EF的长为4, ∴AB+CD=2×4=8. 又∵腰AD的长为5, ∴这个等腰梯形的周长为AB+CD+AD+BC=8+5+5=18. 故选C.查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
已知点O在直线AB上,且线段AB=4cm,线段OB=6cm,E,F分别是OA,OB的中点,则线段EF=_____cm.
2 【解析】因为点O在直线AB上,且线段AB=4cm,线段OB=6cm,所以点O在线段AB延长线上或在线段BA延长线上,当点O在线段AB延长线上,根据中点的性质AO=4+6=10cm,因为点E是OA的中点,所以OE=5cm,点F是OB的中点,OF=3cm,所以EF=5-3=2cm,当点O在线段BA延长线上时,AO=2cm,OB=6cm,因为点E是OA的中点,所以OE=1cm,点F是OB的中点...查看答案和解析>>
科目:初中数学 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:解答题
袋中有外观相同的红球和白球各1个,随机摸出一球记下颜色,放回摇匀后,再随机摸出一球,求两次摸到球的颜色相同的概率是多少?(先画树状图或列表格,再求概率)
【解析】试题分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小明两次摸出的球颜色相同的情况,再利用概率公式即可求得答案. 试题解析: 画树状图得: ∵共有4种等可能的结果,两次摸到的球的颜色相同的有2种情况, ∴两次摸到的球的颜色相同的概率为: .查看答案和解析>>
科目:初中数学 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:填空题
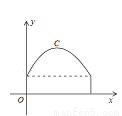
如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线的最高点到路面的距离为6米,该抛物线的函数表达式为 ______ .
查看答案和解析>>
科目:初中数学 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:单选题
三角形两边的长分别是8和6,第三边的长是一元二次方程x2﹣16x+60=0的一个实数根,则该三角形的面积是( )
A. 24 B. 24或8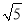 C. 48 D. 8
C. 48 D. 8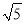
查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年九年级上学期期末试卷数学 题型:解答题
某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10x元(x为整数).
(1)直接写出每天游客居住的房间数量y与x的函数关系式;
(2)设宾馆每天的利润为W元,当每个房间定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
(3)某日,宾馆了解当天的住宿情况,得到以下信息:
①当日所获利润不低于5000元,
②宾馆为游客居住的房间共支出费用没有超过600元,
③每个房间刚好住满2人.
问:这天宾馆入住的游客人数最少有多少人?
(1)y=50-x,(0≤x≤50,且x为整数);(2)每间房价定价为320元时,宾馆每天所获利润最大,最大利润是9000元;(3)20人 【解析】试题分析:(1)根据每天游客居住的房间数量等于50﹣减少的房间数即可解决问题. (2)构建二次函数,利用二次函数的性质解决问题. (3)根据条件列出不等式组即可解决问题. 试题解析:(1)根据题意,得:y=50﹣x,(0≤x≤5...查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年九年级上学期期末试卷数学 题型:单选题
如图,P是⊙O外一动点,PA、PB、CD是⊙O的三条切线,C、D分别在PA、PB上,连接OC、OD.设∠P为x°,∠COD为y°,则y随x的函数关系图象为( )
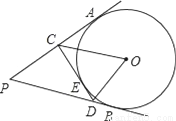
A. 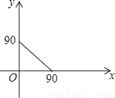 B.
B. 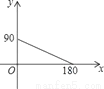
C. 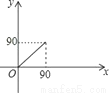 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com