
���������ߵij��ֱ���8��6�������ߵij���һԪ���η���x2��16x+60=0��һ��ʵ��������������ε�����ǣ� ��
A. 24 B. 24��8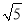 C. 48 D. 8
C. 48 D. 8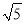

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���Ĵ�ʡ��������Ϫ��2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
���з����У��ǹ���x��һԪ���η��̵�Ϊ�� ��
A. 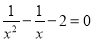 B. x2��2x=(x��1)(x��2)
B. x2��2x=(x��1)(x��2)
C. ax2��bx��c=0 D. (a2��1)x2��bx=0
D �����������������A���Ƿ�ʽ���̣��ʴ�ѡ����� B������ȥ���ŵã�x2+2x=x2-4�������ã�2x=-4��ΪһԪһ�η��̣��ʴ�ѡ����� C��ax2+bx+c=0��a��0��������һԪ���η��̵���ʽ���ʴ�ѡ����� D����Ϊa2��1��0������(a2��1)x2��bx=0�ǹ���x��һԪ���η���. ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
696��ǧ�ף��ÿ�ѧ��������ʾΪ__________ǧ��.
6.96��1010 ����������Ϊ696��ǧ��=69600000000ǧ��,���ÿ�ѧ��������ʾΪ6.96��1010,�ʴ�Ϊ: 6.96��1010.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017��2018ѧ����ѧ�ھ��꼶��ѧ��ĩ�Ծ� ���ͣ������
��ͼ����֪������y=x2+bx+c��x�ύ��A��B���㣨��A�ڵ�B����ࣩ��y�ύ�ڵ�C��0��-3�����Գ�����ֱ��x=1��ֱ��BC�������ߵĶԳ��ύ�ڵ�D����EΪy����һ���㣬CE�Ĵ�ֱƽ���߽���������P��Q���㣨��P�ڵ������ޣ�
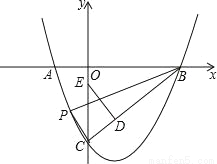
��1���������ߵĺ�������ʽ��ֱ��BC�ĺ�������ʽ��
��2������CDE��ֱ�������Σ��ҡ�CDE=90�� ʱ�������P�����ꣻ
��3������PBC�����Ϊ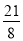 ʱ�����E�����꣮
ʱ�����E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017��2018ѧ����ѧ�ھ��꼶��ѧ��ĩ�Ծ� ���ͣ������
�����������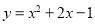 ����ƽ�ƣ�ʹ������ԭ�㣬��ô���������ߵı���ʽ�� ��
����ƽ�ƣ�ʹ������ԭ�㣬��ô���������ߵı���ʽ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017��2018ѧ����ѧ�ھ��꼶��ѧ��ĩ�Ծ� ���ͣ���ѡ��
����ͼ���У�������Գ�ͼ���������ĶԳ�ͼ�ε��ǣ� ��
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩ�Ծ���ѧ ���ͣ������
�����Ŀڴ���װ�аס��ơ���������ɫ��ƹ������ɫ�������ͬ�������а�����2����������1�����ִ�����������һ���ǰ���ĸ���Ϊ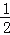 ��
��
��1�������������ĸ�����
��2����һ��������һ�����Żأ����ڶ�������һ�������û���״ͼ���б����������������ǰ���ĸ��ʣ�
��1��1����2��1/6 �������������������1���ȸ��ݰ���ĸ����ǣ���������������Ȼ������õ�����ܸ�����ȥ����ͻ���ĸ������ɣ� ��2��������״ͼ��֪������12�ֿ��ܽ����������������Ϊ����������2�֣��Ӷ�������������������ǰ���ĸ���. �������� ��1��������Ϊ����4-2-1=1 ��������1�� ��2�� ��ʼ ��һ�� ��1 ��2 �� �� �ڶ���...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ̩����������2017-2018ѧ����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ������
��ͼ��������y=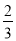 x2+bx+c������B��3��0����C��0����2����ֱ��L��y=��
x2+bx+c������B��3��0����C��0����2����ֱ��L��y=��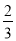 x��
x��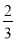 ��y���ڵ�E�����������߽���A��D���㣬PΪ��������һ���㣨����A��D�غϣ���
��y���ڵ�E�����������߽���A��D���㣬PΪ��������һ���㣨����A��D�غϣ���
��1���������ߵĽ���ʽ��
��2������P��ֱ��L�·�ʱ������P��PN��y�ύL�ڵ�N����PN�����ֵ��
��3������P��ֱ��L�·�ʱ������P��PM��x�ύL�ڵ�M����PM�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
�� 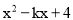 ��һ����ȫƽ��ʽ����k��ֵ��( )
��һ����ȫƽ��ʽ����k��ֵ��( )
A. 2 B. 4 C. -4 D. 4��-4
D �������������������x2-kx+4��һ����ȫƽ��ʽ�� ��k=��4�� ��ѡD.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com