
正六边形的每一个外角是___________度
60°. 【解析】试题分析:∵正六边形的每个外角都相等,并且外角和是360°, ∴正六边形的一个外角的度数为:360°÷6=60°, 故答案为60.科目:初中数学 来源:浙江省杭州市2017-2018学年七年级上学期中考试数学试卷 题型:单选题
下列说法,其中正确的个数为( ).
①几个有理数相乘,积的符号由负因数的个数决定;②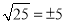 ;③绝对值最小的有理数是
;③绝对值最小的有理数是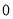 ;④单项式
;④单项式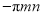 的次数是
的次数是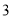 次;⑤
次;⑤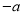 一定在原点的左边.
一定在原点的左边.
A. 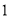 个 B.
个 B. 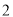 个 C.
个 C. 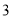 个 D.
个 D. 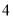 个
个
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2017-2018学年上学期期末考试八年级数学试卷 题型:解答题
先化简: 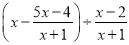 ,再从-1,0,2三个数中任选一个你喜欢的数代入求值.
,再从-1,0,2三个数中任选一个你喜欢的数代入求值.
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2017-2018学年上学期期末考试八年级数学试卷 题型:单选题
如果把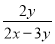 中的x和y都扩大5倍,那么分式的值( )
中的x和y都扩大5倍,那么分式的值( )
A. 不变 B. 扩大5倍 C. 缩小5倍 D. 扩大4倍
A 【解析】试题解析: 分式的值不变. 故选A.查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级上学期第二次月考数学试卷 题型:解答题
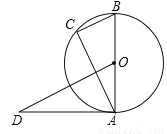
如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD.
(1)若AB=2,OD=3,求BC的长;
(2)若作直线CD,试说明直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,反比例函数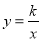 的图象经过点A(2,1),若y≤1,则x的范围为( )
的图象经过点A(2,1),若y≤1,则x的范围为( )
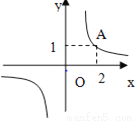
A. x≥1 B. x≥2 C. x<0或0<x≤1 D. x<0或x≥2
D 【解析】试题解析:在第一象限纵坐标为1的以及小于1的函数图象所对应的自变量的取值为 在第三象限纵坐标为1的以及小于1的函数图象所对应的自变量的取值为 故选D.查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级上学期第二次月考数学试卷 题型:单选题
方程x2=4x的根是( )
A. 4 B. ﹣4 C. 0或4 D. 0或﹣4
C 【解析】试题解析: 或 解得: 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:单选题
(2017·辽宁)如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,若CF=1,则AB的长是( )
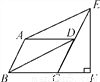
A. 2 B. 1 C. 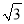 D.
D. 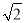
查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:解答题
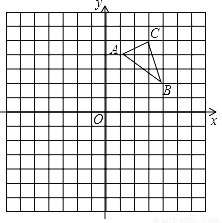
如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度)
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于原点对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出线段OB旋转到OB2扫过图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com