
计算:|﹣3|+(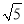 +π)0﹣(﹣
+π)0﹣(﹣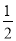 )﹣2.
)﹣2.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2018人教版八年级数学下册练习:期中达标检测卷 题型:填空题
在Rt△ABC中,AC=5,BC=12,则AB边的长是______________.
13或 【解析】试题分析:当AB为斜边时,则AB=;当AB为直角边时,则AB=,则AB边的长为13或.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第一章1.3同底数幂的除法课时练习 题型:解答题
若 xm =2,xn =4,则x2n-3m为多少?
2 【解析】试题分析:先根据幂的乘方法则表示x2n= (xn)2,x3m= (xm)3,再根据同底数幂的除法法则可完成题. 试题解析: ∴x2n-3m= x2n÷x3m =(xn)2÷(xm)3 =16÷8=2.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第一章1.3同底数幂的除法课时练习 题型:单选题
下面计算正确的是( )
A. b6 ÷b5= 2b5 B. b5 + b5 = b10 C. x15÷x5 = x25 D. y10÷y5 = y5
D 【解析】试题解析:A项计算等于b; B项计算等于2b5;C项计算等于x10 ;故D项正确. 故选D.查看答案和解析>>
科目:初中数学 来源:湖南省长沙市2017-2018学年九年级(上)第一次月考数学试卷 题型:解答题
如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
(1)求证:D是BC的中点;
(2)若DE=3,BD﹣AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.

查看答案和解析>>
科目:初中数学 来源:湖南省长沙市2017-2018学年九年级(上)第一次月考数学试卷 题型:填空题
因式分【解析】
2x2﹣18=_____.
查看答案和解析>>
科目:初中数学 来源:湖南省长沙市2017-2018学年九年级(上)第一次月考数学试卷 题型:单选题
(2017四川省巴中市)下列说法正确的是( )
A. “打开电视机,正在播放体育节目”是必然事件
B. 了解夏季冷饮市场上冰淇淋的质量情况适合用普查
C. 抛掷一枚普通硬币,“这枚硬币正面朝上”,这一事件发生的概率为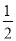
D. 甲、乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是S甲2=0.3,S乙2=0.5,则乙的射击成绩较稳定
C 【解析】试题分析:A、“打开电视机,正在播放体育节目”是随机事件,故此选项错误; B、了解夏季冷饮市场上冰淇淋的质量情况应该采用抽样调查的方式,故此选项错误; C、抛掷一枚普通硬币,“这枚硬币正面朝上”,这一事件发生的概率为,故此选项正确; D、甲、乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是S甲2=0.3,S乙2=0.5,S甲2<S乙2,所以甲的...查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册 第1章 整式的乘除 章节检测题 题型:填空题
若(mx3)·(2xk)=-8x18,则适合此等式的m=______,k=_____.
-4 15 【解析】试题分析:根据单项式的乘法法则,同底数幂相乘,底数不变指数相加的性质计算,再根据系数相等,指数相等列式求解即可. 【解析】 ∵(mx3)•(2xk), =(m×2)x3+k, =﹣8x18, ∴2m=﹣8,3+k=18 解得m=﹣4,k=15.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步训练题 题型:解答题
如图,直线AB、CD、EF相交于点O,∠DOB是它的余角的2倍,∠AOE=2∠DOF,且有OG⊥AB,求∠EOG的度数.
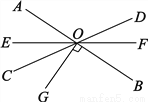
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com