
�ڡ�ABC�У���C=30�㣬��A����B=30�㣬���A= ��
90�� ����������������������������ڽǺ͵õ���A+��B+��C=180�㣬����C=30�㣬��ɼ������A+��B+=150�㣬���ڡ�A����B=30�㣬����ʽ�����ȥ��B������á�A�Ķ����� �������� �ߡ�A+��B+��C=180�㣬��C=30�㣬 ���A+��B+=150�㣬 �ߡ�A����B=30�㣬 ��2��A=180�㣬 ���A=90�㣮 �ʴ�Ϊ90�㣮
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018�괺�˽̰����꼶��ѧ�²����в��� ���ͣ���ѡ��
��ͼ��ͬλ���ǣ�������
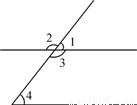
A. ��1�͡�2 B. ��3�͡�4
C. ��2�͡�4 D. ��1�͡�4
D ���������������������ͬλ�ǵĶ����֪��ͼ�С�1�͡�4��ͬλ�ǣ� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�γ���2017-2018ѧ����꼶12���¿���ѧ�Ծ� ���ͣ������
��ֱ֪��y=kx-4��������Χ�ɵ������2����k=____________.
��4 ���������������� �ɺ�������ʽ��֪��ֱ����y�ύ��Ϊ(0����4)�� ��ֱ����x�ύ������Ϊ(x��0) �� �����x=��1�� ����ֱ����x�ύ������Ϊ(1��0)��(��1��0)�� ������Ϊ(1,0)ʱ��k��4=0��k=4�� ������Ϊ(��1,0)ʱ����k��4=0��k=��4�� ��k=��4.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����а�����2016-2017ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ����֪AB��AC����1����2����B����C����BD��CE����˵�����ɣ�
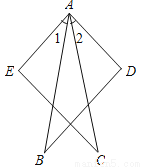
��������
�ߡ�1����2
���1����BAC����2�� ��
�� ����DAB��
�ڡ�ABD�͡�ACE�У�
��B�� (��֪)
��AB�� (��֪)
��EAC�� (��֤)
���ABD�ա�ACE( )
��BD��CE( )
�𰸼����� ��������������������ݡ�1=��2���ɵá�1+��BAC=��2+��BAC����EAC=��DAB��Ȼ�������֪������B=��C��BD=CE������ASA֤����ABD�ա�ACE��Ȼ�����ȫ�������εĶ�Ӧ����ȿ�֤��BD=CE�� ����������ߡ�1=��2 ���1����BAC=��2�� ��BAC �� �� ��EAC =��DAB�� �ڡ�ABD�͡�ACE�У� ��B= ��C (��֪...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����а�����2016-2017ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��֪a��b��8��a2b2��4����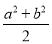 ��ab��___________________________��
��ab��___________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����а�����2016-2017ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
���з�ʽ�У�����ʽ�ǣ�������
A. 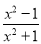 B.
B. 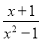 C.
C. 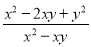 D.
D. 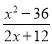
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����в�2017-2018ѧ����꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ������
��ͼ��A��F��E��B�ĵ㹲�ߣ�AC��CE��BD��DF��AE=EF��AC=BD����֤����ACF�ա�BDE��
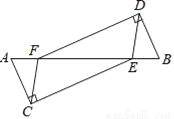
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����в�2017-2018ѧ����꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ���ѡ��
��֪����ͼ��ʾ��AD=AC��BD=BC��OΪAB��һ�㣬��ô��ͼ�й��У���������ȫ�������Σ�
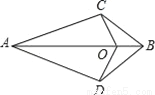
A. 1 B. 2 C. 3 D. 4
C ��������ACO��ACO, ADB��ACB, COB��DOBȫ��.��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2018����꼶��ѧ�ڵ������¿���ѧ�Ծ� ���ͣ���ѡ��
��ͼ����֪����ABCD�ij�ABΪ5����BCΪ4��E��BC���ϵ�һ�����㣬AE��EF��EF��CD�ڵ�F����BE=x��FC=y�����E�ӵ�B�˶�����Cʱ���ܱ�ʾy����x�ĺ�����ϵ�Ĵ���ͼ���ǣ� ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com