
一张桌子有一张桌面和四条桌腿,做一张桌面需要木材0.03 m3,做一条桌腿需要木材0.002m3,现做一批这样的桌子,恰好用去木材3.8m3,共做了多少张桌子?(用多少木料做桌面,多少木料做桌腿,才能使所做的桌面跟桌腿配套)
可做100张这样的桌子. 【解析】试题分析:设共做了x张桌子,则需要的桌面的材料为0.03xm3,桌腿需要木材为4×0.002xm3.根据总木材为3.8m3建立方程求出其解即可. 试题解析:【解析】 设共做了x张桌子,则需要的桌面的材料为0.03xm3,桌腿需要木材为0.002xm3.由题意,得: 0.03x+4×0.002x=3.8,解得:x=100. 答:共做了100...科目:初中数学 来源:福建省三明市大田县2017-2018学年八年级上期末模拟数学试卷 题型:解答题
如图:△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于E,EG⊥AB于G,EF⊥AC交AC的延长线于F,BG与CF的大小关系如何?并证明你的结论.
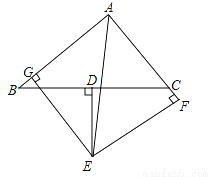
查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市第一学期八年级数学期末复习综合检测卷 题型:单选题
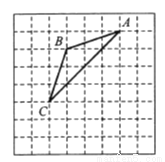
如图,如果把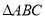 的顶点
的顶点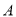 先向下平移3格,再向左平移1格到达
先向下平移3格,再向左平移1格到达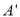 点,连接
点,连接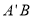 ,那么线段
,那么线段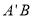 与线段
与线段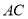 的关系是( )
的关系是( )
A. 垂直 B. 相等 C. 平分 D. 平分且垂直
D 【解析】试题解析:如图,将点A先向下平移3格,再向左平移1格到达A′点,连接A′B,与线段AC交于点O. ∵A′O=OB=,AO=OC=2, ∴线段A′B与线段AC互相平分, 又∵∠AOA′=45°+45°=90°, ∴A′B⊥AC, ∴线段A′B与线段AC互相垂直平分. 故选D.查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上学期第二次月考数学试卷 题型:单选题
如图,AD=AB=BC,那么∠1和∠2之间的关系是 ( )
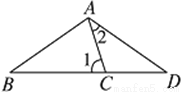
A. ∠1=∠2
B. 2∠1+∠2=180°
C. ∠1+3∠2=180°
D. 3∠1-∠2=180°
D 【解析】试题分析:根据题意得:∠1=∠2+∠D,∠B=∠D,∠1=∠BAC,根据△ABD的内角和可得:∠D=(180-∠BAC-∠2)÷2=(180-∠1-∠2)÷2,∴∠1=∠2+(180-∠1-∠2)÷2,∴3∠1-∠2=180°.查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上学期第二次月考数学试卷 题型:单选题
若分式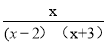 有意义,则 x 的取值范围是( ).
有意义,则 x 的取值范围是( ).
A. x ≠2 B. x ≠2或 x ≠-3 C. x ≠-3 D. x ≠2且 x ≠-3
D 【解析】当分母(x?2)(x+3)≠0,即x≠2、且x≠?3时,分式有意义; 故选D.查看答案和解析>>
科目:初中数学 来源:江苏省实验学校2017-2018学年七年级上学期第二次月检测数学试卷 题型:解答题
解方程(1)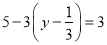 (2)
(2) 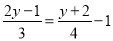
查看答案和解析>>
科目:初中数学 来源:江苏省实验学校2017-2018学年七年级上学期第二次月检测数学试卷 题型:填空题
把如图所示的图形折成一个正方体的盒子,折好后与“顺”相对的字是______.
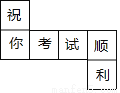
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省白银市中考数学二模试卷 题型:解答题
已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
【解析】 (1)△ABC是等腰三角形,理由见解析; (2)△ABC是直角三角形,理由见解析; (3)x1=0,x2=﹣1. 【解析】试题分析:(1)直接将x=-1代入得出关于a,b的等式,进而得出a=b,即可判断△ABC的形状; (2)利用根的判别式进而得出关于a,b,c的等式,进而判断△ABC的形状; (3)利用△ABC是等边三角形,则a=b=c,进而代入方程求出...查看答案和解析>>
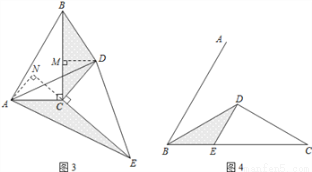
科目:初中数学 来源:重庆市江津区2017届九年级下学期期末考试数学试卷 题型:解答题
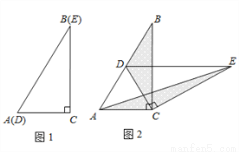
如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现:如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,
①△ADC是 三角形;
②设△BDC的面积为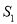 ,△AEC的面积为
,△AEC的面积为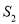 ,则
,则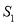 与
与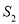 的数量关系是 .
的数量关系是 .
(2)猜想论证:当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中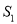 与
与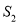 的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究:如图4,已知∠ABC=60°,点D是角平分线上一点,且BD=CD=4,DE∥AB交BC于点E.若在射线BA上存在点F,使S△DCF=S△BDE,请直接写出相应的BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com