
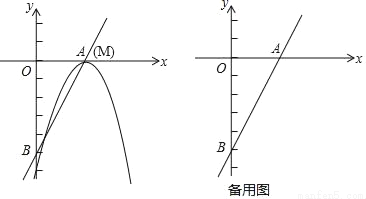
��ֱ֪��y=2x��5��x���y��ֱ��ڵ�A�͵�B��������y=��x2+bx+c�Ķ���M��ֱ��AB�ϣ�����������ֱ��AB����һ������ΪN��
��1����ͼ������M���A�غ�ʱ���������ߵĽ���ʽ��
��2���ڣ�1���������£����N��������߶�MN�ij���
��3��������y=��x2+bx+c��ֱ��AB��ƽ�ƣ��Ƿ���ڵ�M��ʹ�á�OMN���AOB���ƣ������ڣ�ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����2017-2018ѧ�����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
Ϊ�����ֳ��У��γ��н��Գ������ɵ������̻����ƻ���ijһ�ι�·��һ��ȫ�����Ϲ�����Ҫ��·�����˸���һ�ã�����ÿ�������ļ����ȣ����ÿ��6����1�ã�������ȱ22�ã����ÿ��7����1�ã��������������꣮��ԭ������x�ã�����������г�������ȷ���ǣ� ��
A. 6��x��22����7��x��1�� B. 6��x��22��1����7��x��1��
C. 6��x��22��1����7x D. 6��x��22����7x
B �������������������ԭ������x�ã������ס�β���˾���������ÿ���6����һ�ã���ȱ��22�ã���֪��һ�ι�·��Ϊ6��x+22��1������ÿ��7����1�ã��������������꣬��֪��һ�ι�·���ֿ��Ա�ʾΪ7��x��1�������ݹ�·�ij��Ȳ����г����̼��ɣ� �������� ��ԭ������x�ã�������� 6��x+22��1��=7��x��1���� ��ѡ��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��������п���ѧģ���Ծ���1�� ���ͣ���ѡ��
����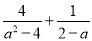 ��•w=1����w=��������
��•w=1����w=��������
A. a+2��a�٩�2�� B. ��a+2��a��2�� C. a��2��a��2�� D. ��a��2��a�٩�2��
D ����������=== �֡ߣ���•w=1�� ��w=?a?2. ��ѡ��D.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�갲��ʡ�п���ѧģ���Ծ� ���ͣ������
��ͼ����Rt��ABC�У���C=90�㣬��B=70�㣬��ABC������Բ��O���AB��BC��CA�ֱ������ڵ�D��E��F�����DEF�Ķ���Ϊ �㣮
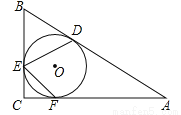
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�갲��ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
���и����У�����ͬ������ǣ�������
A. 52��25 B. ��ab��ba
C. 0.2a2b�멁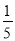 a2b D. a2b3�멁a3b2
a2b D. a2b3�멁a3b2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��������Ǹ����п���ѧģ���Ծ� ���ͣ������
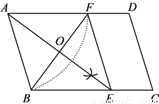
��ͼ����ƽ���ı���ABCD�У���ֱ�ߺ�Բ������BAD��ƽ���߽�BC�ڵ�E���߹���ͼ�ĺۼ�������ͼ���ˣ��� ����EF��
��1����֤���ı���ABEFΪ���Σ�
��2��AE��BF�ཻ�ڵ�O����BF=6��AB=5����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��������Ǹ����п���ѧģ���Ծ� ���ͣ������
ij��������Ϊ-4��,һ��ʳƷ��Ҫ��-28�����,���ÿСʱ����3��,����_____Сʱ���ܽ�����Ҫ����¶�.
8 �����������⿼�����������Ļ�������Ӧ�� �����ڵ��¶ȼ�ȥʳƷ��Ҫ���¶ȣ����Ӧ�����¶ȣ�����ÿСʱ�ܽ���4�棬���������Ҫ��ʱ�䣮 ������ã���Сʱ���� ����Ҫ8Сʱ���ܽ��������¶ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ����������У2017-2018ѧ�����꼶��ѧ������������ѧ�Ծ� ���ͣ������
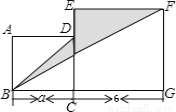
��ͼ��������ABCD��������ECGF�ı߳��ֱ�Ϊa��6��
(1) д����ʾ��Ӱ��������Ĵ���ʽ�����Ҫ��
(2) ��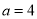 ʱ����Ӱ���ֵ������
ʱ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����2017-2018ѧ�����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ���ѡ��
����ȥ���ŵĽ���У���ȷ���ǣ�������
A. ��3��x��1��=��3x+3 B. ��3��x��1��=��3x��1
C. ��3��x��1��=��3x��3 D. ��3��x��1��=��3x+1
A ����������������� A.��ȷ. ��ѡA.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com