练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

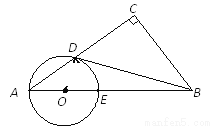
    已知：如图，在RtΔABC中，∠C=90°，点0在AB上，以O为圆心，OA长为半径的圆与AC,AB分别交于点D,E，且∠CBD=∠A．判断直线BD与⊙O的位置关系，并证明你的结论.

    相切，证明见解析. 【解析】试题分析：直线BD与⊙O的位置关系是相切；连接OD，由AE是⊙O的直径，在Rt△ABC中，∠C=90°，易证得DE∥BC，又由∠CBD=∠A，可证得∠ODE+∠EDB=90°，即可证得结论． 试题解析：【解析】 直线BD与⊙O相切．证明如下： 如图，连接OD，ED． ∵OA=OD， ∴． ∵ ∴． 又∵， ∴． ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型：

    如图，等腰三角形ABC中，已知AB＝AC，∠A＝30°，AB的垂直平分线交AC于D，则∠CBD的度数为（ ）

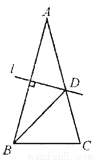
    A. 50° B. 30° C. 75° D. 45°

    D 【解析】因为AB＝AC，∠A＝30°，所以∠ABC=(180°-30°)÷2=75°， 因为AB的垂直平分线交AC于D，所以DA=DB，所以∠A=∠DBA=30°. 所以∠CBD=∠ABC-∠ABD=75°-30°=45°. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型：填空题

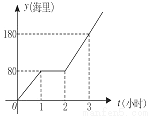
    钓鱼岛自古就是中国领土，中国政府已对钓鱼岛开展常态化巡逻.某天，为按计划准点到达指定海域，某巡逻艇凌晨1：00出发，匀速行驶一段时间后，因中途出现故障耽搁了一段时间，故障排除后，该艇加快速度仍匀速前进，结果恰好准点到达.如图是该艇行驶的路程（海里）与所用时间t（小时）的函数图象，则该巡逻艇原计划准点到达的时刻是 .

    7：00。 【解析】根据函数图象和题意可以求出开始的速度为80海里/时，故障排除后的速度是100海里/时，设计划行驶的路程是a海里，就可以由时间之间的关系建立方程求出路程，再由路程除以速度就可以求出计划到达时间： 由图象及题意，得：故障前的速度为：80÷1=80海里/时，故障后的速度为：（180－80）÷1=100海里/时． 设航行额全程由a海里，由题意，得，解得：a=480。 ...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（3）测试 题型：单选题

    圆外一点P，PA、PB分别切⊙O于A、B，C为优弧AB上一点，若∠ACB=a，则∠APB=（ ）

    A. 180°- 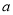B. 90°- 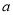C. 90°+ 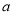D. 180°-2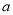

    D 【解析】连接OA,OB,如图, 因为PA,PB分别切⊙O于A,B, 所以OA⊥PA,OB⊥PB, 所以∠OAP=∠OBP=90°, 所以∠AOB=180°－∠P, 因为∠AOB=2∠ACB=2a, 所以2a=180°－∠P, 所以∠P=180°－2a, 故选D.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（2）练习 题型：填空题

    如图所示，在直角坐标系中，A点坐标为（-3，-2），⊙A的半径为1，P为x轴上一动点，PQ切⊙A于点Q，则当PQ最小时，求P点的坐标为___________.

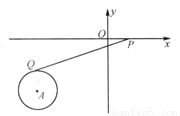
    （-3，0） 【解析】连接AQ,AP, 根据切线的性质定理,得AQ⊥PQ, 要使PQ最小,只需AP最小, 则根据垂线段最短,则作AP⊥x轴于P,即为所求作的点P, 此时P点的坐标为(－3,0),故答案为: (－3,0).

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（2）练习 题型：单选题

    若∠OAB=30°，OA=10cm，则以O为圆心，6cm为半径的圆与射线AB的位置关系是（）

    A. 相交 B. 相切 C. 相离 D. 不能确定

    A 【解析】试题分析：圆心O到直线L的距离为d，圆的半径为r：当时，直线与圆相离；当时，直线与圆相切；当时，直线与圆相交. 由题意得点O到直线AB的距离为5 则以O为圆心,6cm为半径的圆与直线AB 的位置关系是相交 故选A.

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级数学 第十二章 全等三角形 检测题（附答案） 题型：填空题

    如图，等腰直角三角形ABC的直角顶点B在直线PQ上，AD⊥PQ于点D，CE⊥PQ于点E，且AD=1.7cm,DB=3.3cm,则梯形ADEC的面积是________cm2.

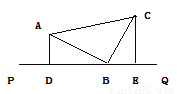
    12.5 【解析】因为AD⊥PQ，CE⊥PQ，所以∠ADB=∠BEC=90°， 因为∠ABC=90°，所以∠ABD+∠EBC=90°， 因为∠ABD+∠BAD=90°，所以∠BAD=∠EBC. 又因为AB=CB，所以△ABD≌△BCE，所以AD=BE，BD=CE. 所以DE=BD+BE=3.3+1.7=5. 所以梯形ADEC的面积为：(AD+CE)×DE÷2=(...

    查看答案和解析>>

    科目：初中数学 来源：同步练习3：1.1菱形的性质与判定 题型：解答题

    判断：菱形的对角线互相垂直平分.（ ）

    对 【解析】 试题分析：根据菱形的性质即可判断. 菱形的对角线互相垂直平分，本题正确.

    查看答案和解析>>

    科目：初中数学 来源：浙江杭州西湖区第十三中学2017-2018学年八年级上学期中考试数学试卷（含解析） 题型：解答题

    （）如图①，在中，，点在上，且，求的度数．

    （）如图②，点，在射线上，点，在射线上，且．

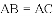
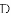
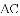
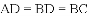
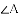
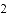
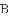
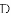
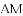
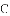
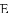
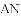
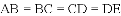
    ①若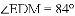，求的度数．

    ②若以为圆心，为半径作弧，与射线上没有交点（除点外），直接写出的取值范围．

    （1）；（2）①；②． 【解析】试题分析：（1）设∠A=x，根据已知条件依次表示出∠ABD、∠BDC、∠C、∠ABC、∠DBC的度数，再利用△DBC内角和为180°，列出方程，解出x即可；（2）设∠A=x，依次表示出∠ACB、∠CBD、∠DCE、∠DEC的度数，再由∠EDM=∠A+∠AED列方程，解出x即可；（3）分析可得，∠EDM≥90°，∠CBD＜90°，∠ECD＜90°，∠A＜90°，...

    查看答案和解析>>

    同步练习册答案