
计算: 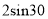 °
°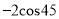 °
°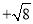 .
.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:北京市丰台区2017-2018学年七年级上学期期末考试数学试卷(WORD版) 题型:单选题
由美国主题景点协会(TEA)和国际专业技术与管理咨询服务提供商AECOM的经济部门合作撰写的2016年《主题公园指数和博物馆指数报告》中显示,中国国家博物馆以7550000的参观人数拔得头筹,成为全世界人气最旺、最受欢迎的博物馆.请将7550000用科学记数法表示为( )
A. 755×104 B. 75.5×105 C. 7.55×106 D. 0.755×107
C 【解析】试题分析:科学计数法是指: ,且,n为原数的整数位数减一,故选C.查看答案和解析>>
科目:初中数学 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:解答题
已知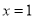 是关于x的方程
是关于x的方程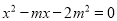 的一个根,求
的一个根,求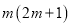 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:北京市海淀区2018届九年级上学期期末考试数学试卷 题型:单选题
抛物线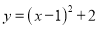 的对称轴是( )
的对称轴是( )
A. 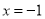 B.
B. 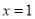 C.
C. 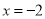 D.
D. 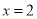
查看答案和解析>>
科目:初中数学 来源:2018年1月北京市海淀区初三上数学期末试卷 题型:解答题
古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究:如图(图1中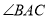 为锐角,图2中
为锐角,图2中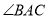 为直角,图3中
为直角,图3中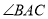 为钝角).
为钝角).
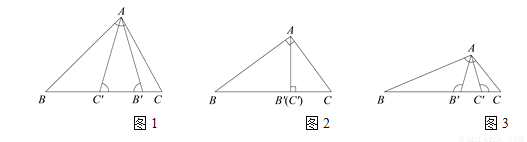
在△ABC的边BC上取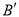 ,
, 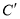 两点,使
两点,使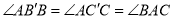 ,则
,则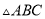 ∽
∽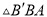 ∽
∽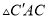 ,
, 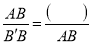 ,
, 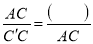 ,进而可得
,进而可得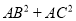
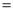 ;(用
;(用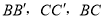 表示)
表示)
若AB=4,AC=3,BC=6,则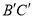
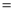 .
.
查看答案和解析>>
科目:初中数学 来源:2018年1月北京市海淀区初三上数学期末试卷 题型:填空题
如图,抛物线 的对称轴为
的对称轴为 ,点P,点Q是抛物线与x轴的两个交点,若点P的坐标为(4,0),则点Q的坐标为__________.
,点P,点Q是抛物线与x轴的两个交点,若点P的坐标为(4,0),则点Q的坐标为__________.

查看答案和解析>>
科目:初中数学 来源:2018年1月北京市海淀区初三上数学期末试卷 题型:单选题
如图,△OAB∽△OCD,OA:OC 3:2,∠A
3:2,∠A α,∠C
α,∠C β,△OAB与△OCD的面积分别是
β,△OAB与△OCD的面积分别是 和
和 ,△OAB与△OCD的周长分别是
,△OAB与△OCD的周长分别是 和
和 ,则下列等式一定成立的是( )
,则下列等式一定成立的是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
若A(x,3)关于y轴的对称点是B(-2,y),则x=____ ,y=______ .
2 3 【解析】由题意得:x=-(-2)=2,y=3. 故答案为(1)2;(2)3.查看答案和解析>>
科目:初中数学 来源:2016-2017学年第二学期无锡市惠山区初一数学期末试卷 题型:解答题
因式分【解析】
(1) ;(2)
;(2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com