
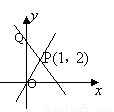
过点Q(0,4)的一次函数的图象与正比例函数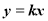 的图象相交于点P(1,2),则这个一次函数图象的解析式是( ).
的图象相交于点P(1,2),则这个一次函数图象的解析式是( ).
A.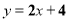 B.
B.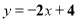
C.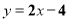 D.
D.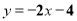
科目:初中数学 来源:2017年甘肃省白银市中考数学二模试卷 题型:单选题
在相同时刻的物高与影长成比例,如果高为1.5m的测杆的影长为2.5m,那么影长为30m的旗杆的高是( )
A. 20m B. 16m C. 18m D. 15m
C 【解析】试题分析:设旗杆的高是Xm,因为在相同时刻的物高与影长成比例,所以,解得x=18m,故选:C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(C卷) 题型:填空题
若一次函数y=kx-3与y=x+1的图象以及y轴围成的三角形的面积为8,则k=________
0或2. 【解析】由一次函数y=kx-3的解析式可知它与y轴的交点纵坐标为-3,因此两直线与y轴的交点间的距离为4.根据两条直线与y轴围成的三角形面积为8,可得出两个函数交点横坐标的绝对值为4.将其代入直线y=x+1中,可求得交点坐标,然后再将交点坐标代入直线y=kx-3中,可求得k的值. 解答:【解析】 设一次函数y=kx-3与y=x+1的图象与y轴的交点分别为A、B,两函数的交点...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(A卷) 题型:解答题
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(1)作出格点△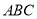 关于直线DE对称的△
关于直线DE对称的△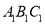 ;(2)作出△
;(2)作出△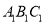 绕点
绕点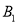 顺时针方向旋转
顺时针方向旋转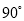 后的△
后的△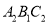 ;(3)△
;(3)△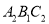 的周长为_____;(保留根号)
的周长为_____;(保留根号)
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(A卷) 题型:填空题
若线段AB平行于x轴,AB长为5,若A的坐标为(4,5),则B的坐标为_________.
(-1,5)或(9,5). 【解析】本题考查了平面直角坐标系. 由AB平行于x轴可知,A、B两点纵坐标相等,再根据线段AB的长为5,B点可能在A点的左边或右边,分别求B点坐标. (-2,3) 【解析】 ∵AB∥x轴, ∴A、B两点纵坐标相等,都是5, 又∵A的坐标是(4,5),线段AB的长为5, ∴当B点在A点左边时,B的坐标为(-1,5), 当B点在A点右边...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(A卷) 题型:单选题
下列交通标志图案是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:填空题
甲、乙、丙三人进行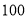 米赛跑,假设每人速度不变,当甲距离终点
米赛跑,假设每人速度不变,当甲距离终点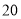 米时,乙比甲落后
米时,乙比甲落后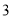 米,丙比乙落后
米,丙比乙落后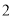 米,那么乙到达终点时,丙离终点的距离为__________米.
米,那么乙到达终点时,丙离终点的距离为__________米.
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:单选题
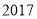 年
年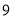 月
月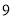 日,第二届“未来科学大奖”中,量子通信卫星“墨子号”首席科学家浙江东阳人潘建伟荣获“物质科学奖”和
日,第二届“未来科学大奖”中,量子通信卫星“墨子号”首席科学家浙江东阳人潘建伟荣获“物质科学奖”和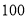 万美元,其中数
万美元,其中数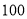 万用科学记数法可表示为( ).
万用科学记数法可表示为( ).
A. 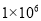 B.
B. 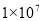 C.
C. 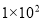 D.
D. 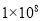
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(C卷) 题型:单选题
如图∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,下面四个结论:①∠ABE=∠BAD,
②△CBE≌△ACD ,③AB=CE, ④AD-BE=DE,其中正确有( )

A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】 ∵∠BEF=∠ADF=90°,∠BFE=∠AFD∴①∠ABE=∠BAD正确; ∵∠1+∠2=90°,∠2+∠CAD=90°,∴∠1=∠CAD, 又∠E=∠ADC=90°,AC=BC,∴②△CEB≌△ADC正确, ∴CE=AD,BE=CD, ∴④AD?BE=DE.正确 而③不能证明, 故选:C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com