练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知， Rt△ABC中，∠C=90°，AD平分∠BAC交BC于D，若BC=32，且BD∶CD=9∶7，则D到AB的距离为( )。

    A. 18 B. 16 C. 14 D. 12

    C 【解析】试题分析：过点D作DE⊥AB于E，根据比例求出CD的长，再根据角平分线上的点到角的两边的距离相等可得DE=CD，得到答案． 【解析】 过点D作DE⊥AB于E， ∵BC=32，BD：CD=9：7， ∴CD=32×=14， ∵∠C=90°，DE⊥AB，AD平分∠BAC， ∴DE=CD=14， 即D到AB的距离为14． 故选：C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷（七） 题型：解答题

    通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的。下面是一个案例，请补充完整。

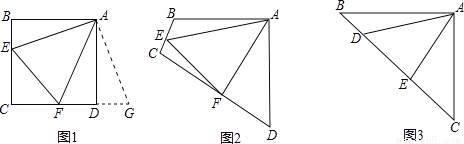
    原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由。

    （1）思路梳理

    ∵AB=CD，

    ∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合。

    ∵∠ADC=∠B=90°，

    ∴∠FDG=180°，点F、D、G共线。

    根据___________，易证△AFG≌__________，得EF=BE+DF。请写出完整证明过程。

    （2）类比引申

    如图2，四边形ABCD中，AB=AD，∠BAD=90°，点E、F分别在边BC、CD上，∠EAF=45°。

    若∠B、∠D都不是直角，则当∠B与∠D满足等量关系_____________时，仍有EF=BE+DF。

    （3）联想拓展

    如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°。猜想BD、DE、EC应满足的等量关系，并写出推理过程。

    （1）SAS，△AFE（2）∠B+∠D=180°（3）猜想：DE2=BD2+EC2 【解析】试题分析：（1）把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合，再证明△AFG≌△AFE进而得到EF=FG，即可得EF=BE+DF； （2）∠B+∠D=180°时，EF=BE+DF，与（1）的证法类同； （3）根据△AEC绕点A顺时针旋转90°得到△ABE′，根据旋转的性质...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省白银市中考数学二模试卷 题型：填空题

    如图，在半径为5cm的⊙O中，弦AB=6cm，OC⊥AB于点C，则OC=_____．

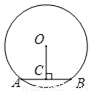
    4cm 【解析】【解析】 连接OA，∵OC⊥AB，∴AC=AB=3cm，∴OC==4（cm）．故答案为：4cm．

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年八年级12月月考数学试卷 题型：解答题

    计算：

    （1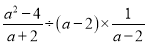）； （2）．

    （1）；（2）． 【解析】试题分析：（1）根据分式的混合运算，先对分式的分子分母因式分解，然后再把除法化为乘法计算，最后约分即可； （2）先通分，再加减，最后约分化简即可. 试题解析：（1）； = = （2） = = =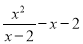

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年八年级12月月考数学试卷 题型：单选题

    如图，在△ABC中，∠A=36°，AB=AC，AB的垂直平分线OD交AB于点O，交AC于点D，连接BD．有下列结论：①∠C=2∠A；②BD平分∠ABC；③S△BCD=S△BOD．其中正确的选项是（　　）

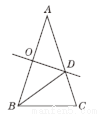
    A. ①③ B. ②③ C. ①②③ D. ①②

    D 【解析】①、∵∠A=36°，AB=AC，∴∠C=∠ABC=72°， ∴∠C=2∠A，正确； ②、∵DO是AB垂直平分线，∴AD=BD。 ∴∠A=∠ABD=36°。∴∠DBC=72°﹣36°=36°=∠ABD。 ∴BD是∠ABC的角平分线，正确； ③，根据已知不能推出△BCD的面积和△BOD面积相等，错误； 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷（C卷） 题型：解答题

    （1）如图，在四边形ABCD中，AB=AD，∠B=∠D=90°，E、F分别是边BC、CD上的点，且∠EAF=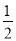∠BAD．求证：EF=BE+FD；

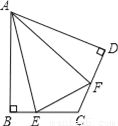
    （2）如图，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是边BC、CD上的点，且∠EAF=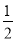∠BAD，（1）中的结论是否仍然成立？

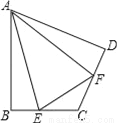
    （3）如图，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，E、F分别是边BC、CD延长线上的点，且∠EAF=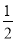∠BAD，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．

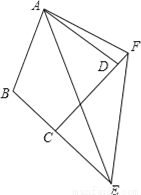
    （1）证明见解析；（2）（2）（1）中的结论EF=BE+FD仍然成立；（3）结论EF=BE+FD不成立，应当是EF=BE﹣FD，证明见解析． 【解析】试题分析：（1）可通过构建全等三角形来实现线段间的转换．延长EB到G，使BG=DF，连接AG．目的就是要证明三角形AGE和三角形AEF全等将EF转换成GE，那么这样EF=BE+DF了，于是证明两组三角形全等就是解题的关键．三角形ABE和AEF中...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷（C卷） 题型：填空题

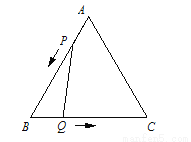
    如图，△ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，点P的速度都是1cm/s，点Q的速度都是2cm/s当点P到达点B时，P、Q两点停止．当t=______________时，△PBQ是直角三角形．

    或 【解析】（1） （2） 综上述，t=

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷（A卷） 题型：解答题

    （8分）如图，△AOB、△COD是等腰直角三角形，点D在AB上．

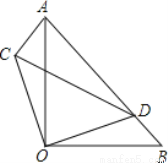
    （1）求证：△AOC≌△BOD；

    （2）若AD=3，BD=1，求CD和△ABC的面积．

    （1）详见解析；（2）． 【解析】 试题分析：（1）因为∠AOB=∠COD=90°，由等量代换可得∠DOB=∠AOC，又因为△AOB和△COD均为等腰直角三角形，所以OC=OD，OA=OB，则△AOC≌△BOD；（2）由（1）可知△AOC≌△BOD，所以AC=BD=1，∠CAO=∠DBO=45°，由等量代换求得∠CAB=90°，根据勾股定理即可求出CD的长． 试题解析:（ 1）证...

    查看答案和解析>>

    科目：初中数学 来源：浙江杭州拱墅区文澜中学2017-2018学年七年级上学期中考试数学试卷（含解析） 题型：单选题

    中国古代数学著作《算法统宗》中有这样一段记载：“三百七十八里关，初健步不为难，次日脚痛减一半，六朝才得到其关．”其大意是，有人要去某关口，路程378里，第一天健步行走，第二天起，由于脚痛，每天走的路程都为前一天的一半，一共走了六天才到达目的地，则此人第六天走的路程为（ ）

    A．24里 B．12里 C．6里 D．3里

    C 【解析】 试题分析：设第一天走了x里，则根据题意知，解得x=192，故最后一天的路程为里. 故选：C

    查看答案和解析>>

    同步练习册答案