
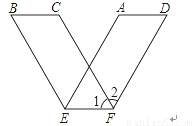
用平行四边形纸条沿对边AB、CD上的点E、F所在的直线折成V字形图案,已知图中∠1=62°,则∠2的度数是________
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:填空题
元旦欢会,班长对全班学生爱吃哪几种水果作了调查,为了确定买什么水果,最值得关注的应该是统计调查数据的________ (填“中位数”、“平均数”或“众数”)
众数 【解析】试题解析:由于众数是数据中出现次数最多的数,故班长最值得关注的应该是统计调查数据的众数. 故答案为:众数.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册 第1-3章 综合测试卷 题型:解答题
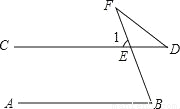
如图,AB∥CD,∠B=78°,∠D=32°,求∠F的度数.
查看答案和解析>>
科目:初中数学 来源:人教版七年级下册 第1-3章 综合测试卷 题型:单选题
下列图形中,能由∠1+∠2=180°得到AB∥CD的是( )
A. 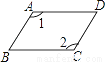 B.
B. 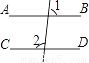
C. 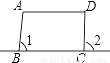 D.
D. 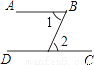
查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:解答题
我们把分子为1的分数叫做单位分数,如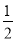 ,
, 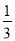 ,
, 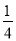 ,…任何一个单位分数都可以拆分成两个不同的单位分数的和,如
,…任何一个单位分数都可以拆分成两个不同的单位分数的和,如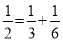 ,
, 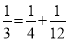 ,
, 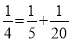 ,…
,…
(1)根据对上述式子的观察,你会发现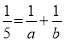 ,则a=________,b=________;
,则a=________,b=________;
(2)进一步思考,单位分数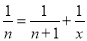 (n是不小于2的正整数),则x=________(用n的代数式表示)
(n是不小于2的正整数),则x=________(用n的代数式表示)
(3)计算: 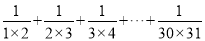 .
.
查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:填空题
请从4a2,(x+y)2,1,9b2中,任选两式做差得到的一个式子进行因式分解是________
4a2﹣1=(2a﹣1)(2a+1) 【解析】根据平方差公式,得, 4a2-1=(2a)2-12=(2a-1)(2a+1), 故答案为:4a2-1=(2a-1)(2a+1).答案不唯一.查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:单选题
如图所示,已知AB∥CD,∠A=50°,∠C=∠E.则∠C等于( )
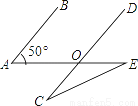
A. 20° B. 25° C. 30° D. 40°
B 【解析】∵AB∥CD,∠A=50°, ∴∠1=∠A=50°, ∵∠C=∠E,∠1=∠C+∠E, ∴∠C=1/2∠1=1/2×50°=25°. 故答案为:B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.2 实际问题与反比例函数(第2课时) 题型:解答题
在某一电路中,保持电压不变,电流 I(安培)和电阻 R(欧姆)成反比例,当电阻 R=5欧姆时,电流 I=2安培.
(1)求 I与 R之间的函数关系式;
(2)当电流 I=0.5时,求电阻 R的值;
(3)若电阻的最大值为欧姆20,请你写出电流的范围.
(1) I= ;(2) R=20;(3)电流的范围是大于等于0.5安培. 【解析】试题分析: (1)由题意可设,代入 R=5,I=2即可求得的值,从而可得I与 R之间的函数关系式; (2)将I=0.5代入(1)中所得函数关系式即可求得对应的R的值; (3)将电阻R最大=20代入(1)中所得函数关系式即可求得对应的的电流I的最小值,由此即可电流I的取值范围. 试题解析:...查看答案和解析>>
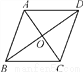
科目:初中数学 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:填空题
如图,在菱形ABCD中,AC,BD相交于点O,若∠BCO=55°,则∠ADO=____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com