
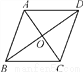
如图,在菱形ABCD中,AC,BD相交于点O,若∠BCO=55°,则∠ADO=____________.
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:填空题
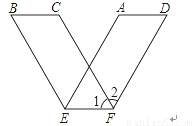
用平行四边形纸条沿对边AB、CD上的点E、F所在的直线折成V字形图案,已知图中∠1=62°,则∠2的度数是________
查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:填空题
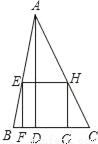
如图,△ABC的内接正方形EFGH中,EH∥BC,其中BC=4,高AD=6,则正方形的边长为_____.
查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:单选题
如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
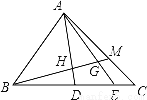
A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
D 【解析】连接EM, ∵CE:CD=CM:CA=1:3 ∴EM平行于AD ∴△BHD∽△BME,△CEM∽△CDA ∴HD:ME=BD:BE=3:5,ME:AD=CM:AC=1:3 ∴AH=(3﹣)ME, ∴AH:ME=12:5 ∴HG:GM=AH:EM=12:5 设GM=5k,GH=12k, ∵BH:HM=3:2=BH:17k ...查看答案和解析>>
科目:初中数学 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:填空题
如图,正方形ABCD的边长为2,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是 .
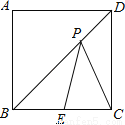
查看答案和解析>>
科目:初中数学 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:单选题
下列命题中,错误的是( )
A. 平行四边形的对角线互相平分
B. 菱形的对角线互相垂直平分
C. 矩形的对角线相等且互相垂直平分
D. 角平分线上的点到角两边的距离相等
C 【解析】试题分析:根据平行四边形的性质对A进行判断;根据菱形的性质对B进行判断;根据矩形的性质对C进行判断;根据角平分线的性质对D进行判断. 【解析】 A、平行四边形的对角线互相平分,所以A选项的说法正确; B、菱形的对角线互相垂直平分,所以B选项的说法正确; C、矩形的对角线相等且互相平分,所以C选项的说法错误; D、角平分线上的点到角两边的距离相等,所以D选...查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
如图,抛物线y=ax 2+bx+c的顶点为M(1,4),与x轴的右交点为A,与y轴的交点为B,点C与点B关于抛物线的对称轴对称,且S△ABC =3.
(1)求抛物线的解析式;
(2)点D是y轴上一点,将点D绕C点逆时针旋转90°得到点E,若点E恰好落在抛物线上,请直接写出点D的坐标;
(3)设抛物线的对称轴与直线AB交于点F,问:在x轴上是否存在点P,使得以P、A、F为顶点的三角形与△ABC相似?若存在,求点P的坐标;若不存在,请说明理由
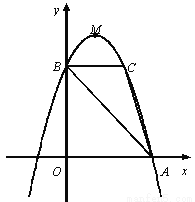
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:单选题
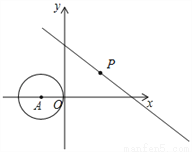
如图,在直角坐标系中,⊙A的圆心A的坐标为(﹣1,0),半径为1,点P为直线y=﹣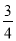 x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是( )
x+3上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是( )
A. 3 B. 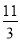 C.
C. 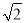 D. 2
D. 2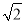
查看答案和解析>>
科目:初中数学 来源:北师大版七年级上册数学全册综合测试卷 题型:填空题
若|a﹣1|+(b+2)2=0,则a+b=________
-1 【解析】【解析】 由题意得:a-1=0,b+2=0,解得:a=1,b=-2.故a+b=1-2=-1.故答案为:-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com