
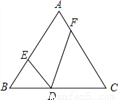
如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.
【答案】(1)证明见解析;(2) 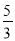
【解析】试题分析:
(1)由题意可得,∠B=∠C=60°,∠BDE+∠CDF=120°,∠BDE+∠BED=120°,由此可得:∠CDF=∠BED,从而可得:△BDE∽△CFD;
(2)由△BDE∽△CFD可得: 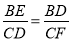 ,由已知易得:CD=BC-BD=5-1=4,由此可得:
,由已知易得:CD=BC-BD=5-1=4,由此可得: 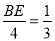 ,解得BE=
,解得BE=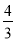 .
.
试题解析:
(1)∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BDE+∠BED=120°.
∵∠EDF=60°,
∴∠BDE+∠CDF=120°,
∴∠CDF=∠BED,
∴△BDE∽△CFD;
(2)∵等边△ABC的边长为5,BD=1,
∴CD=BC-BD=4.
∵△BDE∽△CFD,
∴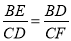 ,即
,即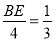 ,
,
∴BE=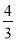 .
.
点睛:本题解题的关键是:由∠EDF=∠B=60°,得到∠BDE+∠BED=120°和∠BDE+∠CDF=120°,从而得到∠BED=∠CDF.
【题型】解答题
【结束】
25
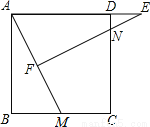
如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.
科目:初中数学 来源:2017年秋人教版数学九年级上册 第23章 旋转 全章测试卷 题型:单选题
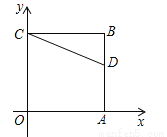
如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,10)
B.(-2,0)
C.(2,10)或(-2,0)
D.(10,2)或(-2,0)
C. 【解析】 试题解析:∵点D(5,3)在边AB上, ∴BC=5,BD=5-3=2, ①若顺时针旋转,则点D′在x轴上,OD′=2, 所以,D′(-2,0), ②若逆时针旋转,则点D′到x轴的距离为10,到y轴的距离为2, 所以,D′(2,10), 综上所述,点D′的坐标为(2,10)或(-2,0). 故选C.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.1图形的旋转(1)测试 题型:填空题
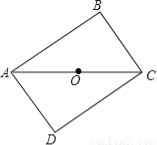
如图所示,将△ABC绕AC的中点O顺时针旋转180°得到△CDA,添加一个条件
,使四边形ABCD为矩形.
查看答案和解析>>
科目:初中数学 来源:人教版八年级上册数学第13章13.3《等腰三角形》 题型:填空题
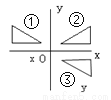
已知直线yy′⊥xx′,垂足为O,则图形①与图形_____成轴对称
查看答案和解析>>
科目:初中数学 来源:人教版八年级上册数学第13章13.3《等腰三角形》 题型:单选题
等腰三角形的对称轴,最多可以有( )
A. 1条 B. 3条 C. 6条 D. 无数条
B 【解析】一般等腰三角形有一条,即底边上的中线所在直线;若是特殊的等腰三角形即等边三角形,则有三条,即每条边上的中线所在直线. 故选:B.查看答案和解析>>
科目:初中数学 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:解答题
解方程:(1) 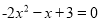 ; (2)
; (2)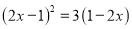 .
.
【答案】(1)x1 =1 ,x2=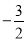 ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=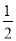 .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: 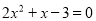 ,
,
方程左边分解因式得: 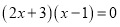 ,
,
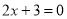 或
或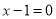 ,
,
解得: 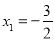 ,
, 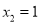 .
.
(2)原方程可化为: 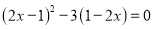 ,即
,即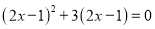 ,
,
∴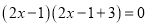 ,
,
∴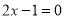 或
或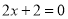 ,
,
解得: 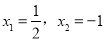 .
.
【题型】解答题
【结束】
20
已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
(1)m的值为6;(2)17. 【解析】试题分析: (1)由题意和根与系数的关系可得:x1+x2=2(m+1),x1x2=m2+5;由(x1-1)(x2-1)=28,可得:x1x2-(x1+x2)=27;从而得到:m2+5-2(m+1)=27,解方程求得m的值,再由“一元二次方程根的判别式”进行检验即可得到m的值; (2)①当7为腰长时,则方程的两根中有一根为7,代入方程可解得m...查看答案和解析>>
科目:初中数学 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:填空题
已知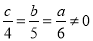 ,则
,则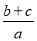 的值为 .
的值为 .
【答案】1.5
【解析】设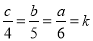 ,则
,则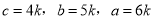 ,
,
∴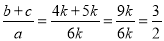 .
.
【题型】填空题
【结束】
13
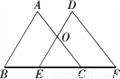
如图,△ABC经过平移到△DEF位置,它们的重叠部分的面积是△ABC的一半,若BC=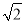 ,则BE= .
,则BE= .
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:单选题
用长8m的铝合金制成如图所示形状的矩形窗框,使窗户的透光面积最大,那么这个窗户的最大透光面积是()

A. 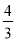 m2 B.
m2 B. 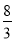 m2 C. 4m2 D.
m2 C. 4m2 D. 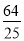 m2
m2
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:解答题
三角形纸片ABC中,∠C=90°,AC=1,BC=2.按图①的方式在这张纸片中剪去一个尽可能大的正方形,称为第1次剪取,记余下的两个三角形面积和为S1;按图②的方式在余下的Rt△ADF和Rt△BDE中,分别剪去尽可能大的正方形,称为第2次剪取,记余下的两个三角形面积和为S2;继续操作下去…….
(1)如图①,求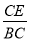 和S1的值;
和S1的值;
(2)第n次剪取后,余下的所有三角形面积之和Sn为________.
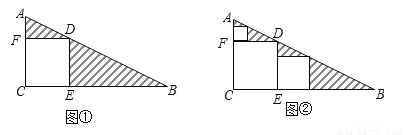
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com