
如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.

(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,求PM+PN的值.
【答案】(1)22.5°,(2)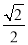 .
.
【解析】
试题分析:(1)由正方形的性质得到,∠BCD=90°,∠DBC=45°,推出AB=BE,根据三角形的内角和定理求出∠BCE=∠BEC=67.5°,根据∠DCE=∠DCB-∠BCE即可求出答案.
(2)连接BP,作EF⊥BC于F,则∠EFB=90°,得出△BEF是等腰直角三角形,从而求得BF=EF=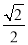 ,然后根据S△BPE+S△BPC=S△BEC,求得PM+PN=EF,即可求得.
,然后根据S△BPE+S△BPC=S△BEC,求得PM+PN=EF,即可求得.
试题解析:(1)在正方形ABCD中,∠BCD=90°,∠DBC=45°,
∵BE=BC,
∴AB=BE,
∴∠BCE=∠BEC=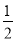 (180°-∠DBC)=67.5°,
(180°-∠DBC)=67.5°,
∴∠DCE=∠DCB-∠BCE=90°-67.5°=22.5°,
(2)连接BP,作EF⊥BC于F,则∠EFB=90°,
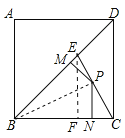
∵∠EBF=45°,
∴△BEF是等腰直角三角形,
∵BE=BC=1,
∴BF=EF=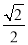 ,
,
∵PM⊥BD,PN⊥BC,
∴S△BPE+S△BPC=S△BEC,
即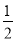 BE•PM+
BE•PM+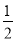 BC•PN=
BC•PN=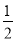 BC•EF,
BC•EF,
∵BE=BC,
∴PM+PN=EF=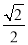 .
.
考点:1.正方形的性质;2.等腰直角三角形.
【题型】解答题
【结束】
28
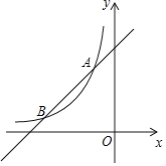
如图,一次函数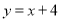 的图像与反比例函数
的图像与反比例函数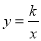 (
(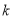 为常数,且
为常数,且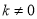 )的图像交于
)的图像交于
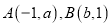 两点.
两点.
(1)求反比例函数的表达式;
(2)在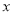 轴上找一点
轴上找一点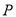 ,使
,使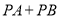 的值最小,求满足条件的点
的值最小,求满足条件的点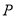 的坐标;
的坐标;
(3)在(2)的条件下求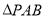 的面积.
的面积.
科目:初中数学 来源:河北省邯郸市2017-2018学年八年级下学期第一次月考数学试卷B4(含答案) 题型:单选题
如图,为测量池塘边A、B两点的距离,小明在池塘的一侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=14m,则A、B间的距离是( )
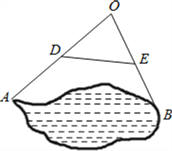
A. 18m B. 24m C. 28m D. 30m
查看答案和解析>>
科目:初中数学 来源:2018年湖北省十堰市丹江口市中考数学模拟试卷(3月份) 题型:单选题
某校举行“汉字听写比赛”,5个班级代表队的正确答题数如图.这5个正确答题数所组成的一组数据的中位数和众数分别是( )
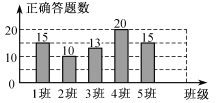
A. 10,15 B. 13,15 C. 13,20 D. 15,15
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017-2018学年第二学期八年级期中数学模拟试卷 题型:解答题
如图,四边形ABCD中AB∥CD,对角线AC,BD相交于O,点E,F分别为BD上两点,且BE=DF,∠AEF=∠CFB.
(1)求证:四边形ABCD是平行四边形;
(2)若AC=2OE,试判断四边形AECF的形状,并说明理由.

【答案】(1)(2)见解析
【解析】试题分析:(1)已知AB∥CD,根据两直线平行,内错角相等可得∠ABD=∠CDB,由∠AEF=∠CFB,根据平角的定义可得∠AEB=∠CFD,利用ASA证得△ABE≌△CDF,根据全等三角形的性质可得AB=CD,由AB∥CD,根据一组对边平行且相等的四边形为平行四边形即可得四边形ABCD是平行四边形;(2)平行四边形AECF是矩形,根据平行四边形的性质可得OB=OD ,OA=OC= AC,由BE=DF证得OE=OF,根据对角线互相平分的四边形为平行四边形可判定四边形AECF是平行四边形,再证得AC=EF,根据对角线相等的平行四边形是矩形即可判定平行四边形AECF是矩形.
AC,由BE=DF证得OE=OF,根据对角线互相平分的四边形为平行四边形可判定四边形AECF是平行四边形,再证得AC=EF,根据对角线相等的平行四边形是矩形即可判定平行四边形AECF是矩形.
试题解析:
(1)证明:∵AB∥CD,
∴∠ABD=∠CDB,
又∵∠AEF=∠CFB,
∴∠AEB=∠CFD,
又∵BE=DF,
∴△ABE≌△CDF(ASA),
∴AB=CD,
又∵AB∥CD,
∴四边形ABCD是平行四边形;
(2) 平行四边形AECF是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD ,OA=OC= AC,
AC,
∵BE=DF,
∴OB﹣BE=DO﹣DF,
∴OE=OF,
又∵OA=OC,
∴四边形AECF是平行四边形,
又∵AC=2OE,EF=2OE,
∴AC=EF,
∴平行四边形AECF是矩形.
【题型】解答题
【结束】
23
已知,  ,
, 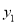 与
与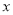 成正比例,
成正比例, 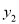 与
与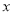 成反比例,并且当
成反比例,并且当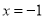 时,
时, 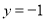 ,当
,当 时,
时, 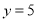 .
.
(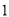 )求
)求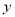 关于
关于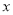 的函数关系式.
的函数关系式.
(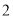 )当
)当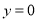 时,求
时,求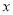 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017-2018学年第二学期八年级期中数学模拟试卷 题型:填空题
如图,
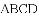
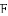
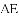
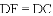


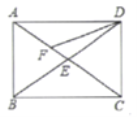
【答案】57.5
【解析】∵四边形ABCD是矩形,∴∠ADC=90°,
∵∠ADF=25°,∴∠CDF=∠ADC?∠ADF=90°?25°=65°,
∵DF=DC,∴∠ECD= .
.
故答案为:57.5°.
【题型】填空题
【结束】
16
关于 的方程
的方程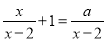 有增根,则
有增根,则 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级下学期第一次月考数学试卷 题型:解答题
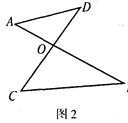
如图,图1是△ABC,图2是“8字形”(将线段AB、CD相交于点O,连接AD、CB形成的图形),图3是一个五角星形状,试解答下列问题:
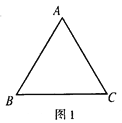
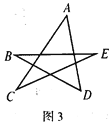
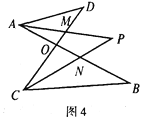
(1)图1的△ABC中,∠A+∠B+∠C=_____,并证明你写出的结论;(要有推理证明过程)
(2)图2的“8字形”中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:_____;
(3)若在图2的条件下,作∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N(如图4).请直接写出∠P与∠D、∠B之间数量关系:____;
(4)图3中的点A向下移到线段BE上时,请直接写出∠CAD+∠B+∠C+∠D+∠E=____.
查看答案和解析>>
科目:初中数学 来源:青岛版九年级下册数学 第6章事件的概率 单元检测 题型:单选题
一个口袋中有红球、白球共20只,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一只球,记下它的颜色后再放回,不断重复这一过程,共摸了50次,发现有30次摸到红球,则估计这个口块中有红球大约多少只?( )
A.8只 B.12只 C.18只 D.30只
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com