
����˵����ȷ���ǣ� ��
A. ������OA��3 cm B. �߶�AB���߶�BA����ͬһ���߶�
C. ��A��ֱ��l��λ�ù�ϵ������ D. ����ֱ���ཻ��3������
C ���������������������ƽ��ͼ�εĻ����������η�����ѡ��������ж�. A.������һ���˵㣬������һ���������죬B.�߶�AB���߶�BA��ͬһ���߶Σ�D.����ֱ���ཻ��1��2��3�����㣬�ʴ��� C.��A��ֱ��L��λ�ù�ϵ�����֣�����ֱ���Ϻ͵���ֱ���⣬��ѡ����ȷ.
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������������2017-2018ѧ�������һѧ����ѧ��ĩ�Ծ� ���ͣ������
���㣺��1��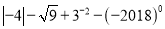 ��
��
��2��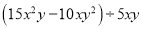 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������к�����2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ����D��E�ڡ�ABC�ı�BC�ϣ���ABD�ա�ACE������B��CΪ��Ӧ���㣬D��EΪ��Ӧ���㣬���н��۲�һ���������ǣ� ��
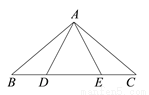
A. AC=CD B. BE=CD C. ��ADE=��AED D. ��BAE=��CAD
A ���������ߡ�ABD�ա�ACE�����ADB=��AEC����BAD=��CAE��BD=CD�� ��180��-��ADB=180��-��AEC����BAD+��DAE=��CAE+��DAE��BD+DE=CE+DE�� ����ADE=��AED����BAE=��CAD��BE=CD�� ��B��C��Dѡ��������ʲ��������⣻ ��֤��AC=CD����A�������⣬ ��ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ������
��ͼ��һ���������չ��ͼ������������ϵ����ֻ�Ϊ��������b=______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ���ѡ��
���з��̵ı����У���ȷ���ǣ�������
A. ����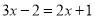 �������
�������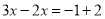
B. ����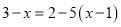 ��ȥ���ţ���
��ȥ���ţ���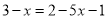
C. ����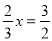 ��δ֪��ϵ����Ϊ1����
��δ֪��ϵ����Ϊ1����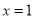
D. ����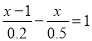 ����
����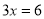
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ��ѧ����ĩ����Ծ� ���ͣ������
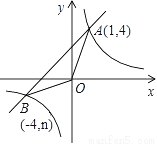
��ͼ����֪����������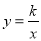 ��ͼ����һ�κ���
��ͼ����һ�κ���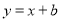 ��ͼ���ڵ�A��1��4������B����4��n����
��ͼ���ڵ�A��1��4������B����4��n����
(1)��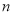 ��
��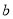 ��ֵ��
��ֵ��
(2)���OAB�������
(3)ֱ��д��һ�κ���ֵ���ڷ���������ֵ���Ա���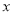 ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ��ѧ����ĩ����Ծ� ���ͣ������
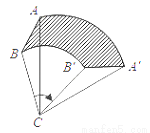
��ͼ������ABC�Ƶ�C��ת60��õ���A��B��C�䣬��֪AC=6��BC=4�����߶�ABɨ��ͼ�Σ���Ӱ���֣������Ϊ______________����������У�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ��ѧ����ĩ����Ծ� ���ͣ���ѡ��
��������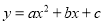 ��
��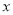 ����������������ǣ���1��0���ͣ�2��0������������ߵĶԳ�����ֱ�ߣ�������
����������������ǣ���1��0���ͣ�2��0������������ߵĶԳ�����ֱ�ߣ�������
A. 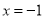 B.
B. 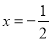 C.
C. 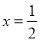 D.
D. 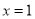
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ2017-2018ѧ����꼶��ѧ�ڵڶ���ѧ������ѧ�Ծ� ���ͣ���ѡ��
�ҹ�ֽɡ����������ʮ�������ͼ��ɡ�������ſ�������£������AE=AF��DE=DF�����AED�ա�AFD�������ǣ� ��
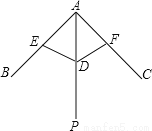
A. SAS B. ASA C. AAS D. SSS
D ����������AE=AF��DE=DF��AD�ǡ�AED�͡�AFD�Ĺ����ߣ� ���AED�ա�AFD��SSS��. ��ѡD.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com