练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    现代互联网技术的广泛应用，催生了快递行业的高度发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同．

    （1）求该快递公司投递总件数的月平均增长率；

    （2）如果平均每人每月最多可投递0.6万件，那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？

    （1）该快递公司投递总件数的月平均增长率为10%；（2）该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务，至少需要增加2名业务员． 【解析】试题分析：（1）设该快递公司投递总件数的月平均增长率为x，根据“今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同”建立方程，解方程即可； （2）首先求出今年6月份的快递...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    （1）计算：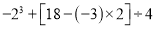

    （2）化简求值.2(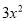－5y)－[－3(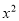－3y)] ，其中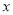=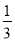，y=-2

    （3）解方程：

    （1）-2；（2）原式=9x2-19y=39；（3）x=-3.2. 【解析】试题分析: （1）根据有理数的混合运算法则进行运算． （2）根据乘法分配律先去括号再合并同类项化简，然后代入求值． （3）此题先去分母，再去括号，然后移项合并同类项求解． 试题解析: 【解析】 （1）原式=-8+（18+6）÷4=-8+6=-2 （2）【解析】 原式=6x2-10y+...

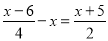
    查看答案和解析>>

    科目：初中数学 来源：内蒙古赤峰市宁城县2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    下列四个数中，最小的数是（ ）

    A. -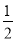 B. 0 C. -2 D. 2

    C 【解析】试题解析：∵-2＜-＜0＜2， ∴四个数中最小的数是-2. 故选C．

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省2017-2018学年九年级数学上学期期末试卷 题型：单选题

    已知x1、x2是关于x的一元二次方程x2－(2m＋3)x＋m2＝0的两个不相等的实数根，且满足x1＋x2＝m2，则m的值是(　　)

    A. －1 B. 3 C. 3或－1 D. －3或1

    B 【解析】试题解析：根据题意得△=（2m+3）2-4m2＞0，解得m＞-； 根据根与系数的关系得x1+x2=2m+3， 则2m+3=m2， 整理得m2-2m-3=0，即（m-3）（m+1）=0， 解得m1=3，m2=-1， 则m=3．

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省2017-2018学年九年级数学上学期期末试卷 题型：单选题

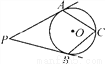
    如图，PA，PB切⊙O于点A，B，点C是⊙O上一点，且∠P＝36°，则∠ACB＝(　　)

    A. 54° B. 72° C. 108° D. 144°

    B 【解析】连接AO,BO,∠P=36°，所以∠AOB=144°，所以∠ACB=72°.故选B.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末模拟数学试卷 题型：填空题

    如图，⊙O的半径为2，点A、C在⊙O上，线段BD经过圆心O，∠ABD=∠CDB=90°，AB=1，CD=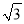，则图中阴影部分的面积为______．

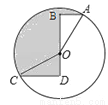
    【解析】试题解析：在Rt△ABO中，∠ABO=90°，OA=2，AB=1， ∴OB= =，sin∠AOB=，∠AOB=30°． 同理，可得出：OD=1，∠COD=60°． ∴∠AOC=∠AOB+（180°-∠COD）=30°+180°-60°=150°． 在△AOB和△OCD中，有 , ∴△AOB≌△OCD（SSS）． ∴S阴影=S扇形OAC． ∴S扇形O...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末模拟数学试卷 题型：单选题

    如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：

    ①4ac＜b2；

    ②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；

    ③3a+c＞0

    ④当y＞0时，x的取值范围是﹣1≤x＜3

    ⑤当x＜0时，y随x增大而增大

    其中结论正确的个数是（　　）

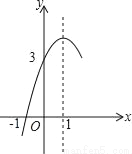
    A. 4个 B. 3个 C. 2个 D. 1个

    B 【解析】解：∵抛物线与x轴有2个交点，∴b2﹣4ac＞0，所以①正确； ∵抛物线的对称轴为直线x=1，而点（﹣1，0）关于直线x=1的对称点的坐标为（3，0），∴方程ax2+bx+c=0的两个根是x1=﹣1，x2=3，所以②正确； ∵x=﹣=1，即b=﹣2a，而x=﹣1时，y=0，即a﹣b+c=0，∴a+2a+c=0，所以③错误； ∵抛物线与x轴的两点坐标为（﹣1，0）...

    查看答案和解析>>

    科目：初中数学 来源：江西省上饶市2017届九年级（上）期末数学试卷（解析版） 题型：填空题

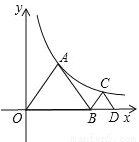
    如图，等边△OAB和等边△BCD的顶点A、C分别在双曲线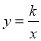的图象上，若OA=1，则点C的坐标为____________．

    （， ）． 【解析】过A作AE⊥OB于E，过C作CF⊥BD于F， ∵△OAB是等边三角形， ∴∠AOB=∠OAB=60°，OB=OA=1， ∴OE=，AE=， ∴k=， ∴双曲线的解析式为y=， 设等边三角形CBD的边长为2a， ∴BF=a，CF=a， ∴C（1+a， a）， ∴（1+a）•a =， ∴a=，（负值舍去）， ∴...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期末检测题 题型：填空题

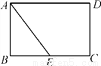
    如图，在矩形ABCD中，E是BC的中点，矩形ABCD的周长是20 cm，AE＝5 cm，则AB的长为____cm.

    4 【解析】试题分析：设AB=xcm，则由矩形ABCD的周长是20cm可得BC=10﹣xcm， ∵E是BC的中点，∴BE=BC=。 在Rt△ABE中，AE=5cm，根据勾股定理，得AB2+BE2=AE2，即x2+（）2=52，解得：x=4。 ∴AB的长为4cm。

    查看答案和解析>>

    同步练习册答案