练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

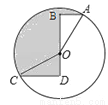
    如图，⊙O的半径为2，点A、C在⊙O上，线段BD经过圆心O，∠ABD=∠CDB=90°，AB=1，CD=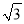，则图中阴影部分的面积为______．

    【解析】试题解析：在Rt△ABO中，∠ABO=90°，OA=2，AB=1， ∴OB= =，sin∠AOB=，∠AOB=30°． 同理，可得出：OD=1，∠COD=60°． ∴∠AOC=∠AOB+（180°-∠COD）=30°+180°-60°=150°． 在△AOB和△OCD中，有 , ∴△AOB≌△OCD（SSS）． ∴S阴影=S扇形OAC． ∴S扇形O...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    在数轴上距-1.5有2个单位长度的点表示的数是________；

    -3.5或0.5 【解析】在数轴上,与?1.5相距2个单位长度的点表示的数是?1.5+2=0.5,?1.5?2=-3.5. 故答案为：-3.5或0.5.

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省2017-2018学年九年级数学上学期期末试卷 题型：解答题

    在一个不透明的口袋中装有3个带号码的球，球号分别为2，3，4，这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏，游戏规则如下：

    先由甲同学从中随机摸出一球，记下球号，并放回搅匀，再由乙同学从中随机摸出一球，记下球号。将甲同学摸出的球号作为一个两位数的十位上的数，乙同学的作为个位上的数。若该两位数能被4整除，则甲胜，否则乙胜.

    问：这个游戏公平吗？请说明理由。

    【解析】 画树状分析图如图： ∵能组成的两位数有22，23，24， 32，33，34，42，43，44，能被4整除的有：24，32，，44。 ∴P（甲胜）=，P（乙胜）=。 ∵P（甲胜）≠P（乙胜），∴这个游戏不公平。 【解析】列表法或树状图法，概率，数的整除性质，游戏公平性。 用列表法或树状图法求出两位数的个数和两位数能被4整除的个数，从而求出甲胜和乙胜的概率，比...

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省2017-2018学年九年级数学上学期期末试卷 题型：填空题

    如图，△ABC内接于⊙O，AB＝BC，∠ABC＝120°，AD为⊙O的直径，AD＝6，那么BC的值为( )

    A. 3 B. 2 C. 3 D. 2

    A 【解析】∵AB=BC， ∴∠BAC=∠C. ∵∠ABC=120°， ∴∠C=∠BAC=30°. ∴∠D=∠C=30°。 ∵AD为直径， ∴∠ABD=90°。 ∵AD=6， ∴AB=AD=3, ∴BC=AB=3. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末模拟数学试卷 题型：解答题

    现代互联网技术的广泛应用，催生了快递行业的高度发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同．

    （1）求该快递公司投递总件数的月平均增长率；

    （2）如果平均每人每月最多可投递0.6万件，那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？

    （1）该快递公司投递总件数的月平均增长率为10%；（2）该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务，至少需要增加2名业务员． 【解析】试题分析：（1）设该快递公司投递总件数的月平均增长率为x，根据“今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同”建立方程，解方程即可； （2）首先求出今年6月份的快递...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末模拟数学试卷 题型：填空题

    已知抛物线y＝ax2＋bx＋c(a≠0)与x轴的两个交点的坐标分别是(－3，0)，(2，0)，则方程ax2＋bx＋c＝0(a≠0)的解是_________.

    .x1＝－3，x2＝2 【解析】试题解析：∵抛物线y＝ax2＋bx＋c(a≠0)与x轴的两个交点的坐标分别是(?3,0)，(2,0)， ∴当x=?3或x=2时，y=0， 即方程的解为 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：江西省上饶市2017届九年级（上）期末数学试卷（解析版） 题型：解答题

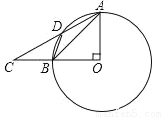
    如图，∠AOB=90°，C在OB的延长线上，D为⊙O上一点，∠BAD=∠BDC．

    （1）求证：CD是⊙O的切线；

    （2）若⊙O的半径为1，且OB=BC，求四边形AOBD的面积．

    （1）证明见解析；（2）． 【解析】试题分析：（1）作直径BE，连接OD、DE，如图，利用圆周角定理得到∠BDE=90°，∠E=∠BAD，由于∠BAD=∠BDC．则∠E=∠BDC，加上∠DBO=∠BDO，则∠BDC+∠BDO=90°，然后根据切线的判定定理可得到CD是⊙O的切线； （2）先根据直角斜边上中线性质得DB=OB=OD，则△OBD为等边三角形，所以S△OBD=， ∠BO...

    查看答案和解析>>

    科目：初中数学 来源：江西省上饶市2017届九年级（上）期末数学试卷（解析版） 题型：单选题

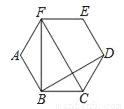
    如图，在正六边形ABCDEF中，△BCD的面积为2，则△BCF的面积为（　　）

    A. 8 B. 6 C. 4 D. 3

    C 【解析】△BCD与△BCF同底，其高的比为：2：1， ∵△BCD的面积为2， ∴△BCF的面积为：4． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期末检测题 题型：填空题

    已知1 mm＝1 000 μm，用科学计数法表示2.5 μm＝____mm.

    2.5×10－3 【解析】2.5μm =0.0025mm=2.5×10?3mm. 故答案为：2.5×10?3.

    查看答案和解析>>

    同步练习册答案