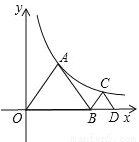
如图.等边△OAB和等边△BCD的顶点A.C分别在双曲线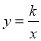的图象上.若OA=1.则点C的坐标为． (. )． [解析]过A作AE⊥OB于E.过C作CF⊥BD于F. ∵△OAB是等边三角形. ∴∠AOB=∠OAB=60°.OB=OA=1. ∴OE=.AE=. ∴k=. ∴双曲线的解析式为y=. 设等边三角形CBD的边长为2a. ∴BF=a.CF=a. ∴C•a =. ∴a=.. 题目和参考答案——青夏教育精英家教网—

如图，等边△OAB和等边△BCD的顶点A、C分别在双曲线的图象上，若OA=1，则点C的坐标为____________．

（，）．【解析】过A作AE⊥OB于E，过C作CF⊥BD于F， ∵△OAB是等边三角形， ∴∠AOB=∠OAB=60°，OB=OA=1， ∴OE=，AE=， ∴k=， ∴双曲线的解析式为y=，设等边三角形CBD的边长为2a， ∴BF=a，CF=a， ∴C（1+a， a）， ∴（1+a）•a =， ∴a=，（负值舍去）， ∴...

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：内蒙古赤峰市宁城县2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

请你根据如图所示已知条件，推想正确结论，

要求：每个结论同时含有字母a，b．

写出至少两条正确结论：①_______________________，②_____________________．

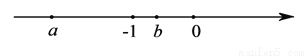
a+b<0 b-a>0 【解析】试题解析：根据有理数的大小比较，有理数的加法，可得a+b<0，或b-a>0.

查看答案和解析>>

科目：初中数学 来源：辽宁省2018届九年级上学期期末模拟数学试卷 题型：解答题

现代互联网技术的广泛应用，催生了快递行业的高度发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同．

（1）求该快递公司投递总件数的月平均增长率；

（2）如果平均每人每月最多可投递0.6万件，那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？

（1）该快递公司投递总件数的月平均增长率为10%；（2）该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务，至少需要增加2名业务员．【解析】试题分析：（1）设该快递公司投递总件数的月平均增长率为x，根据“今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同”建立方程，解方程即可；（2）首先求出今年6月份的快递...

查看答案和解析>>

科目：初中数学 来源：江西省上饶市2017届九年级（上）期末数学试卷（解析版） 题型：解答题

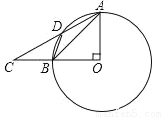
如图，∠AOB=90°，C在OB的延长线上，D为⊙O上一点，∠BAD=∠BDC．

（1）求证：CD是⊙O的切线；

（2）若⊙O的半径为1，且OB=BC，求四边形AOBD的面积．

（1）证明见解析；（2）．【解析】试题分析：（1）作直径BE，连接OD、DE，如图，利用圆周角定理得到∠BDE=90°，∠E=∠BAD，由于∠BAD=∠BDC．则∠E=∠BDC，加上∠DBO=∠BDO，则∠BDC+∠BDO=90°，然后根据切线的判定定理可得到CD是⊙O的切线；（2）先根据直角斜边上中线性质得DB=OB=OD，则△OBD为等边三角形，所以S△OBD=， ∠BO...

查看答案和解析>>

科目：初中数学 来源：江西省上饶市2017届九年级（上）期末数学试卷（解析版） 题型：解答题

计算：．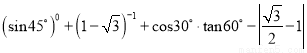

1．【解析】试题分析：利用三角函数，分母有理化，绝对值性质计算. 试题解析： =1++=1+++=1.

查看答案和解析>>

科目：初中数学 来源：江西省上饶市2017届九年级（上）期末数学试卷（解析版） 题型：单选题

如图，在正六边形ABCDEF中，△BCD的面积为2，则△BCF的面积为（　　）

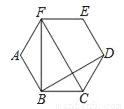
A. 8 B. 6 C. 4 D. 3

C 【解析】△BCD与△BCF同底，其高的比为：2：1， ∵△BCD的面积为2， ∴△BCF的面积为：4．故选C．

查看答案和解析>>

科目：初中数学 来源：北师大版九年级上数学第二章《一元二次方程》单元检测卷 题型：解答题

某商场将进货单价为40元的商品按50元售出时能卖出500个，经过市场调查发现，这种商品最多只能卖500个．若每个售价提高1元，其销售量就会减少10个，商场为了保证经营该商品赚得8 000元的利润而又尽量兼顾顾客的利益，售价应定为多少？这时应进货多少个？

售价应定为每个60元，这时应进货 400个. 【解析】试题分析：利用每件产品的利润乘以总个数得到总利润，解方程. 试题解析：设每个售价提高x元，由题意可得方程：（50+x-40)(500-10x)=8000，整理得：x2-40x+300=0 ，解得：x1=10 , x2=30. 为尽量兼顾顾客的利益，取x=10， 50+10=60 即：售价应...

查看答案和解析>>

科目：初中数学 来源：北师大版九年级上数学第二章《一元二次方程》单元检测卷 题型：单选题

已知方程x2-6x+q=0可以配方成（x-p）2=7的形式，那么x2-6x+q=2可以配方成下列的（）

A. （x-p）2=5 B. （x-p）2=9 C. （x-p+2）2=9 D. （x-p+2）2=5

B 【解析】x2－6x＋q＝0,由题意，方程可配方成(x－p)2＝7的形式，所以(x－p)2-7=0,由 x2－6x＋q＝2, (x－p)2-7=2,所以所以(x－p)2＝9，所以选B.

查看答案和解析>>

科目：初中数学 来源：江西婺源县2016-2017学年九年级上期末考试数学试卷含答案 题型：填空题

用半径为3cm，圆心角是120°的扇形围成一个圆锥的侧面，则这个圆锥的底面半径为______cm．

1．【解析】试题分析：利用圆锥的侧面展开图中扇形的弧长等于圆锥底面的周长，可设此圆锥的底面半径为r，由题意，得2πr=，解得r=1cm．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学