
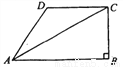
如图,在四边形ABCD中,AB∥DC,∠B=900,连接AC∠DAC=∠BAC.若BC=4cm,AD=5cm,则AB=_______cm.
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源:河南省2017-2018学年八年级上期末模拟数学试卷 题型:填空题
如图,已知AB∥CD,O是∠ACD和∠BAC的平分线的交点,若AC=6,S△AOC=6则AB与CD之间的距离是( ) 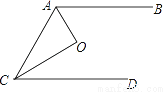
A. 1cm B. 2cm C. 3cm D. 4cm
C 【解析】过点0作AB的垂线,交AB于点D,交CD于点F,过O作OE垂直AC,交AC于点E,由题意得:OD=OE=OF, 6OE=12,解得OE=2,则DF=4.查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期末测试 题型:填空题
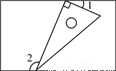
如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上.若∠1=20°,则∠2=____________.
查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:解答题
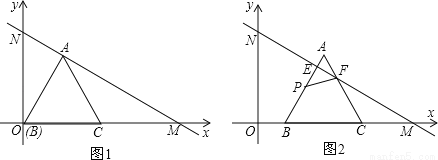
如图1,在平面直角坐标系xOy中,直线MN分别与x轴正半轴、y轴正半轴交于点M、N,且OM=6cm,∠OMN=30°,等边△ABC的顶点B与原点O重合,BC边落在x轴的正半轴上,点A恰好落在线段MN上,如图2,将等边△ABC从图1的位置沿x轴正方向以1cm/s的速度平移,边AB、AC分别与线段MN交于点E、F,在△ABC平移的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿折线B→A→C运动,当点P达到点C时,点P停止运动,△ABC也随之停止平移.设△ABC平移时间为t(s),△PEF的面积为S(cm2).
(1)求等边△ABC的边长;
(2)当点P在线段BA上运动时,求S与t的函数关系式,并写出自变量t的取值范围;
(3)点P沿折线B→A→C运动的过程中,是否在某一时刻,使△PEF为等腰三角形?若存在,求出此时t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:解答题
解下列关于x的不等式(组):
(1) 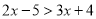 (2)
(2)
(3)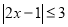 (4)
(4) 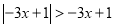
查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:单选题
如图所示,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC.∠EBC=∠E=60°,若BE=6,DE=2,则BC的长度是( )
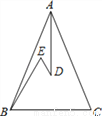
A.6 B.8 C.9 D.10
B 【解析】延长ED交BC于M,延长AD交BC于N,作DF∥BC, ∵AB=AC,AD平分∠BAC, ∴AN⊥BC,BN=CN, ∵∠EBC=∠E=60°, ∴△BEM为等边三角形, ∴△EFD为等边三角形, ∵BE=6,DE=2, ∴DM=4, ∵△BEM为等边三角形, ∴∠EMB=60°, ∵AN⊥BC, ∴∠DNM=90...查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:单选题
△ABC中,AB=AC,BC=10,AB的垂直平分线与AC的垂直平分线分别交BC于点D、E且DE=4,则AD+AE的值为( )
A. 6 B. 10 C. 6或14 D. 6或10
C 【解析】分两种情况: ①如图, ∵D在AB垂直平分线上,E在AC垂直平分线上, ∴BD=AD,CE=AE, ∵BC=10,DE=4, ∴BD+CE=10-4=6, ∴AD+AE=6, ②如图, ∵D在AB垂直平分线上,E在AC垂直平分线上, ∴BD=AD,CE=AE, ∵BC=10,DE=4, ∴BD+CE=BC+DE=1...查看答案和解析>>
科目:初中数学 来源:2017年广西南宁八中中考数学五模试卷 题型:单选题
若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则实数k的取值范围是( )
A. k>﹣1 B. k<1且k≠0 C. k≥﹣1且k≠0 D. k>﹣1且k≠0
D 【解析】试题分析:根据一元二次方程的定义和△的意义得到k≠0且△>0,即(﹣2)2﹣4×k×(﹣1)>0,然后解不等式即可得到k的取值范围k>﹣1且k≠0. 故选D.查看答案和解析>>
科目:初中数学 来源:2016-2017学年黑龙江省哈尔滨市松北区2017届九年级上学期期末数学试卷 题型:解答题
先化简,再求代数式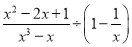 的值,其中x=2
的值,其中x=2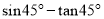 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com