练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

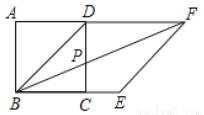
    如图，在正方形ABCD的对角线BD是菱形BEFD的一边，菱形BEFD的对角线交正方形ABCD的一边CD于点P，∠FPC的度数是（ ）

    A．135° B．120° C．112．5° D．67．5°

    C 【解析】 试题分析：因为正方形ABCD的对角线BD是菱形BEFD的一边，菱形BEFD的对角线BF交于P，所以∠DBC=∠BDC=45°，∠DBF=∠FBE=22．5°，所以∠BPD=∠PBC+∠BCP=90°+22．5°=112．5°．所以∠FPC=∠BPD=112．5°．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年八年级数学人教版16.2二次根式定义的乘除同步练习 题型：填空题

    ________；

    【解析】试题解析：原式 故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学第三章圆单元检测卷 题型：填空题

    如图，四边形ABCD内接于⊙O，AB为⊙O的直径，点C为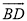的中点．若∠A=40°，则∠B=________度．

    70 【解析】因为∠A=40°，所以∠C=140°, ∠DOB=80°，则∠DBO=50°，∠DBC=20°所以∠CBO=70 度

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学全册综合测试卷 题型：解答题

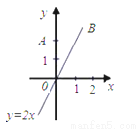
    如图，直线OB是一次函数y=2x的图象，点A的坐标是（0，2），点C在直线OB上且△ACO为等腰三角形，求C点坐标．

    （,），（,），（-,-），C4（,1） 【解析】试题分析：本题要分三种情况进行讨论， 第一种情况：以OA为腰，A为等腰三角形的顶点，那么C点必定在第一象限，且纵坐标的值比A的要大，根据OA=AC我们知道了AC的距离，我们可以根据C的纵坐标和横坐标以及AC的长构成的直角三角形，运用勾股定理以及所在直线的函数关系式求出C的坐标． 第二种情况：以OA为一腰，O为三角形的顶点，那么C点...

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学全册综合测试卷 题型：填空题

    观察下列勾股数

    第一组：3=2×1+1，4=2×1×（1+1），5=2×1×（1+1）+1

    第二组：5=2×2+1，12=2×2×（2+1），13=2×2×（2+1）+1

    第三组：7=2×3+1，24=2×3×（3+1），25=2×3×（3+1）+1

    第四组：9=2×4+1，40=2×4×（4+1），41=2×4×（4+1）+1

    …观察以上各组勾股数组成特点，第7组勾股数是______________（只填数，不填等式）

    15，112，113 【解析】试题分析：根据题意我们通过观察可以得出规律，这类勾股数分别为2n+1，2n(n+1)和2n(n+1)+1，根据规律即可得出第七组的勾股数.

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学全册综合测试卷 题型：单选题

    如图，四边形ABCD是平行四边形，顶点A、B的坐标分别是A（1，0），B（0，﹣2），顶点C、D在双曲线y=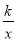上，边AD与y轴相交于点E，S四边形BEDC=5S△ABE=10，则k的值是（　 　）

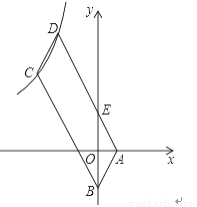
    A. -16                                B. -9 C. -8 D. -12

    D 【解析】试题解析：如图，过C、D两点作x轴的垂线，垂足为F、G，DG交BC于M点，过C点作CH⊥DG，垂足为H， ∵四边形ABCD是平行四边形， ∴∠ABC=∠ADC， ∵BO∥DG， ∴∠OBC=∠GDE， ∴∠HDC=∠ABO， 在△CDH和△ABO中， ， ∴△CDH≌△ABO（AAS）， ∴CH=AO=1，DH=OB=2， ...

    查看答案和解析>>

    科目：初中数学 来源：人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型：解答题

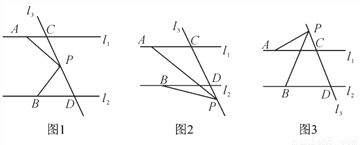
    如图,已知直线l1∥l2，直线l3和直线l1，l2交于点C和D,直线l3上有一点P.

    (1)如图1,若P点在C,D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化,并说明理由；

    (2)若点P在C,D两点的外侧运动时(P点与点C,D不重合,如图2和3)，试直接写出∠PAC,∠APB,∠PBD之间的关系，不必写理由．

    (1)当P点在C，D之间运动时，∠APB＝∠PAC＋∠PBD (2)当点P在C，D两点的外侧运动时，在l2下方时，则∠PAC＝∠PBD＋∠APB；在l1上方时，则∠PBD＝∠PAC＋∠APB. 【解析】试题分析：（1）当P点在C、D之间运动时，首先过点P作PE∥l1，由l1∥l2，可得PE∥l2∥l1，根据两直线平行，内错角相等，即可求得：∠APB=∠PAC+∠PBD． （2）当点P在...

    查看答案和解析>>

    科目：初中数学 来源：人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型：解答题

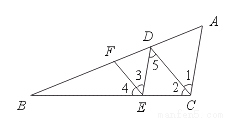
    如图，已知AC∥DE，DC∥EF，CD平分∠BCD．求证：EF平分∠BED．

    证明见解析 【解析】试题分析：先根据平行线的性质得出∠1=∠5，∠5=∠3，得到∠1=∠3，再由平行线的性质得到∠2=∠4，再根据CD平分∠ACB可知∠1=∠2，故可得出结论． 试题解析：证明：∵AC∥DE（已知），∴∠1=∠5． 同理∠5=∠3，∴∠1=∠3． ∵DC∥EF（已知），∴∠2=∠4． ∵CD平分∠ACB，∴∠1=∠2，∴∠3=∠4，∴EF平分∠BED．...

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学全册综合测试卷 题型：填空题

    已知点P（﹣b，2）与点Q（3，2a）关于原点对称，则a= ，b= ．

    ﹣1，3． 【解析】 试题分析：根据两个点关于原点对称时，它们的坐标符号相反，即点P（x，y）关于原点O的对称点是P′（﹣x，﹣y），∵点P（﹣b，2）与点Q（3，2a）关于原点对称， ∴﹣b=﹣3，﹣2=2a，∴b=3，a=﹣1． 故答案为：﹣1，3．

    查看答案和解析>>

    同步练习册答案