
如图,四边形ABCD是平行四边形,顶点A、B的坐标分别是A(1,0),B(0,﹣2),顶点C、D在双曲线y=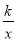 上,边AD与y轴相交于点E,S四边形BEDC=5S△ABE=10,则k的值是( )
上,边AD与y轴相交于点E,S四边形BEDC=5S△ABE=10,则k的值是( )
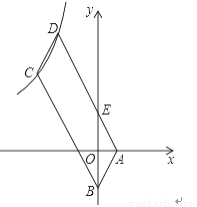
A. -16 B. -9 C. -8 D. -12
D 【解析】试题解析:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H, ∵四边形ABCD是平行四边形, ∴∠ABC=∠ADC, ∵BO∥DG, ∴∠OBC=∠GDE, ∴∠HDC=∠ABO, 在△CDH和△ABO中, , ∴△CDH≌△ABO(AAS), ∴CH=AO=1,DH=OB=2, ... 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017-2018学年八年级数学人教版16.2二次根式定义的乘除同步练习 题型:单选题
若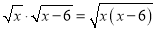 ,则( )
,则( )
A. x≥6 B. x≥0 C. 0≤x≤6 D. x为一切实数
A 【解析】试题解析:根据题意得: 解得: 故选A.查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第三章圆单元检测卷 题型:单选题
如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
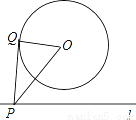
A. 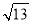 B.
B. 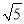 C. 3 D. 2
C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:填空题
如果一个三角形的面积为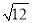 ,一边长为
,一边长为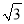 ,那么这边上的髙为________ .
,那么这边上的髙为________ .
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:单选题
如图,在正方形ABCD的对角线BD是菱形BEFD的一边,菱形BEFD的对角线交正方形ABCD的一边CD于点P,∠FPC的度数是( )
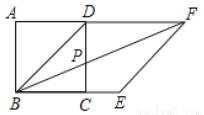
A.135° B.120° C.112.5° D.67.5°
C 【解析】 试题分析:因为正方形ABCD的对角线BD是菱形BEFD的一边,菱形BEFD的对角线BF交于P,所以∠DBC=∠BDC=45°,∠DBF=∠FBE=22.5°,所以∠BPD=∠PBC+∠BCP=90°+22.5°=112.5°.所以∠FPC=∠BPD=112.5°.查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:单选题
下列等式一定成立的是( )
A. 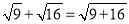 B.
B. 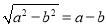
C. 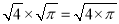 D.
D. 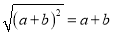
查看答案和解析>>
科目:初中数学 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
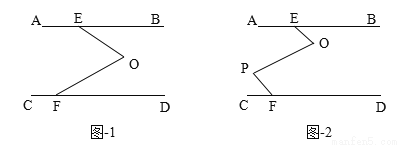
如图1,AB∥CD,EOF是直线AB、CD间的一条折线.
(1)说明:∠O=∠BEO+∠DFO.
(2)如果将折一次改为折二次,如图-2,则∠BEO、∠O、∠P、∠PFC会满足怎样的关系,证明你的结论.
查看答案和解析>>
科目:初中数学 来源:人教版七年级下册 第1-3章 综合测试卷 题型:解答题
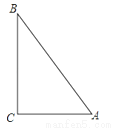
如图,点A表示小雨家,点B表示小樱家,点C表示小丽家,她们三家恰好组成一个直角三角形,其中AC⊥BC,AC=900米,BC=1200米,AB=1500米.
(1)试说出小雨家到街道BC的距离以及小樱家到街道AC的距离.
(2)画出表示小丽家到街道AB距离的线段.
查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:单选题
已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为( )
A. 20°或100° B. 120° C. 20°或120° D. 36°
A 【解析】试题分析:本题难度中等,考查等腰三角形的性质.因为所成比例的内角,可能是顶角,也可能是底角,因此要分类求解. 【解析】 设两内角的度数为x、4x; 当等腰三角形的顶角为x时,x+4x+4x=180°,x=20°; 当等腰三角形的顶角为4x时,4x+x+x=180°,x=30,4x=120; 因此等腰三角形的顶角度数为20°或120°. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com