
化简 的结果为【 】
的结果为【 】
A.﹣1 B.1 C.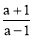 D.
D.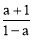
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试七年级数学试卷 题型:解答题
幼儿园智慧树班某次能力测验有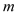 人参加,这次测验共有五道题,并且每人至少做对了一道题每道题至少有一人做对,只做对一道题的有8人,五道题全做对的有27人,只做对两道题的人数是只做三道题的人数的2倍.
人参加,这次测验共有五道题,并且每人至少做对了一道题每道题至少有一人做对,只做对一道题的有8人,五道题全做对的有27人,只做对两道题的人数是只做三道题的人数的2倍.
(1)答对四道题的有n人,那么只做对三道题的人数可以用含m与n的代数式表示为____________;
(2)(1)中的m=42,那么n可以是多少?请说明理由;
(3)统计了每道题做错的人数如下表:
题 号 | 1 | 2 | 3 | 4 | 5 |
做错的人数 | 5 | 8 | 14 | 23 | 45 |
若m=73,请根据上表求n.
(1) (2)1或4;(3)23. 【解析】试题分析: 用总人数减去答对1道题的人数,减去答对4道题的人数,减去答对5道题的人数,得到答对2道题和3道题的人数,根据做对两道题的人数是只做三道题的人数的2倍,即可列出答对3道题的人数. 当时, 中的式子为: , 是正整数,而且是3的倍数,即可求得的值. 根据做错的总题目数列方程,解方程即可. 试题解析:(1). (2)可...查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(北师大版):期中检测题 题型:单选题
如图,在△ABC中AB=AC,BD是∠ABC的平分线,DE∥AB,BE=5 cm,CE=3 cm.则△CDE的周长是( )
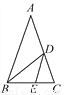
A. 15cm B. 13cm C. 11cm D. 9cm
B 【解析】【解析】 ∵DE∥AB,BD平分∠ABC,∴∠EBD=∠ABD=∠EDB,∴DE=BE=5cm.∵AB=AC,DE∥AB,∴∠C=∠ABE=∠DEC,∴DC=DE=5cm,且CE=3cm,∴DE+EC+CD=5cm+3cm+5cm=13cm,即△CDE的周长为13cm,故选B.查看答案和解析>>
科目:初中数学 来源:重庆市校2017-2018学年八年级上学期第二阶段考试数学试卷 题型:填空题
在△ABC中,AB=6,AC=2,AD是BC边上的中线,则AD的取值范围是________.
2<AD<4 【解析】延长AD至E,使DE=AD,连接CE. 在△ABD和△ECD中, , ∴△ABD≌△ECD(SAS), ∴CE=AB. 在△ACE中,CE﹣AC<AE<CE+AC, 即4<2AD<8, 2<AD<4. 故答案是:2<AD<4.查看答案和解析>>
科目:初中数学 来源:重庆市校2017-2018学年八年级上学期第二阶段考试数学试卷 题型:单选题
如图,在△ABC中,∠C=70°,沿图中虚线截去∠C,则∠1+∠2=( )
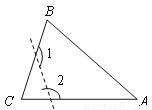
A. 250° B. 360° C. 180° D. 140°
A 【解析】∵在△ABC中,∠C=70°, ∴∠A+∠B=180°-70°=110°, 又∵∠A+∠B+∠1+∠2=360°, ∴∠1+∠2=360°-110°=250°. 故选A.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期中检测题 题型:解答题
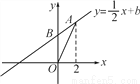
已知平面直角坐标系xOy(如图),直线 y=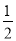 x+b经过第一、二、三象限,与y轴交于点B,点A(2,t)在直线y=
x+b经过第一、二、三象限,与y轴交于点B,点A(2,t)在直线y=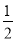 x+b上,连结AO,△AOB的面积等于1.
x+b上,连结AO,△AOB的面积等于1.
(1)求b的值;
(2)如果反比例函数y=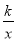 (k是常量,k≠0)的图象经过点A,求这个反比例函数的表达式.
(k是常量,k≠0)的图象经过点A,求这个反比例函数的表达式.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期中检测题 题型:填空题
已知点A(a,b)在双曲线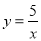 上,若a、b都是正整数,则图象经过B(a,0)、C(0,b)两点的一次函数的解析式(也称关系式)为______.
上,若a、b都是正整数,则图象经过B(a,0)、C(0,b)两点的一次函数的解析式(也称关系式)为______.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第24章小结与复习 测试 题型:解答题
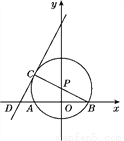
如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为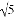 ,AB=4.
,AB=4.
(1)求点B,P,C的坐标;
(2)求证:CD是⊙P的切线.
查看答案和解析>>
科目:初中数学 来源:湖北省大冶市金湖街办2017-2018学年八年级上学期第二次月考(12月)数学试卷 题型:单选题
如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
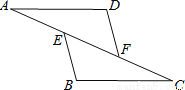
A. ∠A=∠C B. ∠D=∠B C. AD∥BC D. DF∥BE
B 【解析】试题分析:利用全等三角形的判定与性质进而得出当∠D=∠B时,△ADF≌△CBE. 当∠D=∠B时, 在△ADF和△CBE中 ∵, ∴△ADF≌△CBE(SAS)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com