练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列方程中，是关于x的一元二次方程的是（　　）

    A. 2x=1﹣x B. ax2+bx+c=0 C. x2﹣2x﹣1 D. （x﹣1）（x+2）=1

    D 【解析】解：A． 2x=1﹣x 是一元一次方程； B． ax2+bx+c=0 ，当a=0时，不是一元二次方程； C． x2﹣2x﹣1，不是方程； D． （x﹣1）（x+2）=1，是一元二次方程． 故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广东省江门市2017-2018学年八年级12月月考数学试卷 题型：解答题

    解方程：．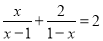

    x=0 【解析】 试题分析：观察可得最简公分母是（x﹣1），方程两边乘最简公分母，可以把分式方程转化为整式方程求解． 试题解析：去分母，得x﹣2=2（x﹣1）， 去括号，得x﹣2=2x﹣2， 移项，合并同类项，得﹣x=0， 系数化为1，得x=0． 检验：把x=0代入（x﹣1）=﹣1≠0． 故原方程的解为x=0．

    查看答案和解析>>

    科目：初中数学 来源：江苏省丹阳市2017-2018学年八年级12月月考数学试卷 题型：填空题

    比较大小：4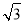 7．（填“＞”、“=”、“＜”）

    ＜． 【解析】 试题解析：∵（4，72=49；48＜49， ∴4＜7，

    查看答案和解析>>

    科目：初中数学 来源：江苏省2018届九年级12月月考数学试卷 题型：填空题

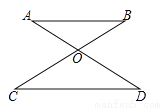
    已知AB∥CD，AD与BC相交于点O．若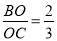，AD=10，则AO=______．

    4． 【解析】∵AB∥CD， 解得，AO=4， 故答案是：4．

    查看答案和解析>>

    科目：初中数学 来源：江苏省2018届九年级12月月考数学试卷 题型：单选题

    设A（﹣2，y1），B（1，y2），C（2，y3）是抛物线y=﹣（x+1）2+1上的三点，则y1，y2，y3的大小关系为（　　）

    A. y1＞y2＞y3 B. y1＞y3＞y2 C. y3＞y2＞y1 D. y3＞y1＞y2

    A 【解析】把A（﹣2，y1），B（1，y2），C（2，y3）代入抛物线有， y1=0，y2=-3，y3=-8， y1＞y2＞y3。 选A.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 21.3实际问题与一元二次方程（1） 测试 题型：填空题

    学校举行乒乓球比赛，有若干个队报名，比赛采取单循环制（每两个队要比赛一场），一共比了66场，则有___________个队参加了报名.

    12 【解析】由题意得=66, , (x-12)(x+11)=0, 解得x1=12，x2=-11 所以有12个队参加了报名.

    查看答案和解析>>

    科目：初中数学 来源：郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型：解答题

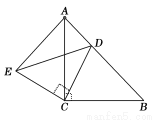
    如图，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，D为AB边上一点，求证：

    （1）△ACE≌△BCD；（2）．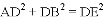

    【答案】（1）证明见解析；（2）证明见解析．

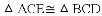
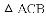
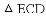
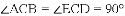
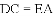
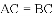
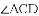
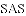
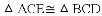
    【解析】试题分析：（1）本题要判定，已知和都是等腰直角三角形，，则，，，又因为两角有一个公共的角，所以，根据得出．

    （2）由（1）的论证结果得出，，．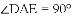

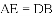
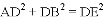    试题解析：

    （1）∵，

    ∴

    ∴．

    ∵，，

    ∴．

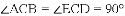
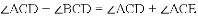
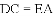
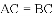
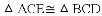
    （2）∵是等腰直角三角形，

    ∴．

    ∵，

    ∴

    ∴，

    ∴．

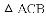
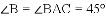
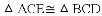
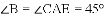
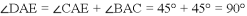
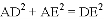    由（1）知AE=DB，

    ∴．

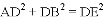    考点：（1）勾股定理；（2）全等三角形的判定与性质；（3）等腰直角三角形．

    【题型】解答题
    【结束】
    20

    已知一次函数y=2x+4

    （1）在如图所示的平面直角坐标系中，画出函数的图象；

    （2）求图象与x轴的交点A的坐标，与y轴交点B的坐标；

    （3）在（2）的条件下，求出△AOB的面积；

    （4）利用图象直接写出：当y＜0时，x的取值范围．

    （1）画图见解析；（2）A（﹣2，0）B（0，4）；（3）4；（4）x＜﹣2． 【解析】试题分析：（1）求得一次函数y=2x+4与x轴、y轴的交点坐标，利用两点确定一条直线就可以画出函数图象；（2）由（1）即可得结论；（3）通过交点坐标根据三角形的面积公式即可求出面积；（4）观察函数图象与x轴的交点就可以得出结论． 试题解析：（1）当x=0时y=4，当y=0时，x=﹣2，则图象如图所示...

    查看答案和解析>>

    科目：初中数学 来源：郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型：单选题

    以下列数组作为三角形的三条边长，其中能构成直角三角形的是( )

    A. 1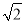， ，3 B. 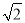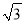， ，5 C. 1.5，2，2.5 D. ， ，

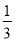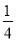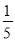
    【答案】C

    【解析】A、12+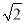（）2≠32，不能构成直角三角形，故选项错误；

    B、(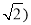2+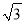（）2≠52，不能构成直角三角形，故选项错误；

    C、1.52+22=2.52，能构成直角三角形，故选项正确；

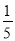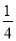    D、（））2+（）2≠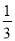（）2，不能构成直角三角形，故选项错误．

    故选：C．

    【题型】单选题
    【结束】
    3

    在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到斜边AB的距离是（ ）

    （A） （B） （C）9 （D）6

    A 【解析】 试题分析：根据题意画出相应的图形，如图所示，在Rt△ABC中，由AC及BC的长，利用勾股定理求出AB的长，然后过C作CD⊥AB，由直角三角形的面积可以由两直角边乘积的一半来求，也可以由斜边AB乘以斜边上的高CD除以2来求，两者相等，即=AC•BC=AB•CD，将AC，AB及BC的长代入求出CD的长，即为C到AB的距离． 故选A

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习（含答案） 题型：解答题

    解方程：x2+10x+16=0.(因式分解法)

    x1=-2,x2=-8 【解析】x2+10x+16=0 (x+2)(x+8)=0 x+2=0,x+8=0; 所以x1=-2,x2=-8.

    查看答案和解析>>

    同步练习册答案