
如图,△ABC中,∠A=70°,AB=4,AC= 6,将△ABC沿图中的虚线剪开,则剪下的阴影三角形与原三角形不相似的是( )
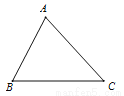
A. 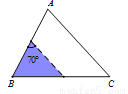 B.
B. 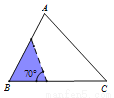
C. 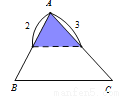 D.
D. 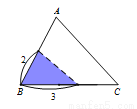
科目:初中数学 来源:江苏省泰兴市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
对于任何有理数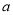 ,下列各式中一定为负数的是
,下列各式中一定为负数的是
A. 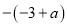 B.
B. 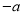 C.
C. 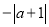 D.
D. 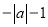
查看答案和解析>>
科目:初中数学 来源:安徽省凤阳县梅市2017-2018学年九年级第一学期期末数学试卷 题型:单选题
已知α是锐角,且点A(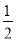 ,a),B(sin30°+cos30°,b), C(-m2+2m-2,c)都在二次函数y=-x2+x+3的图象上,那么a、b、c的大小关系是( )
,a),B(sin30°+cos30°,b), C(-m2+2m-2,c)都在二次函数y=-x2+x+3的图象上,那么a、b、c的大小关系是( )
A. a<b<c B. a<c<b C. b<c<a D. c<b<a
D 【解析】由题意可知抛物线的开口向下,对称轴是x= ,从而可知点A为抛物线的顶点,所以a最大,|sin30°+cos30°-| = ,|-m2+2m-2- |=(m-1)2+ ≥>,抛物线开口向下时离对称轴越近的点的y值越大,故b>c,所以c<b<a;故选D.查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
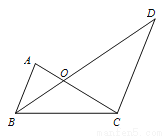
如图,BO是△ABC的角平分线,延长BO至D使得BC=CD.
(1)求证:△AOB∽△COD.
(2)若AB=2,BC=4,OA=1,求OC长.
查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:填空题
扇形半径为3cm,弧长为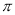 cm,则扇形圆心角的度数为___________________.
cm,则扇形圆心角的度数为___________________.
查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:单选题
将抛物线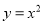 先向左平移2个单位再向下平移1个单位,得到新抛物线的表达式是( )
先向左平移2个单位再向下平移1个单位,得到新抛物线的表达式是( )
A. 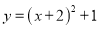 B.
B. 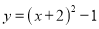
C. 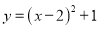 D.
D. 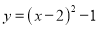
查看答案和解析>>
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:解答题
已知:如图,ABCD是一块边长为2米的正方形铁板,在边AB上选取一点M,分别以AM和MB为边截取两块相邻的正方形板料. 当AM的长为何值时,截取两块相邻的正方形板料的总面积最小?

查看答案和解析>>
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:单选题
为测量某河的宽度,小军在河对岸选定一个目标点A,再在他所在的这一侧选点B,C,D,使得AB⊥BC,CD⊥BC,然后找出AD与BC的交点E.如图所示,若测得BE=90m,EC=45m,CD=60m,则这条河的宽AB等于( )
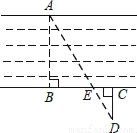
A. 120m B. 67.5m C. 40m D. 30m
A 【解析】∵∠ABE=∠DCE, ∠AEB=∠CED, ∴△ABE∽△DCE, ∴. ∵BE=90m,EC=45m,CD=60m, ∴ 故选A.查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
如图,将一副直角三角板如图放置,若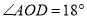 ,则
,则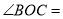 __度.
__度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com