练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列各式中，与(a-1)2一定相等的是（ ）

    A. a2+1 B. a2-1 C. a2-2a -1 D. a2-2a+1

    D 【解析】试题分析：完全平方公式：. ，故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市2018届九年级（上）入学数学试卷（9月份） 题型：单选题

    关于x的一元二次方程mx2+2x+1=0有两个不相等的实数根，则m的取值范围是（　　）

    A. m＜1 B. m≤1 C. m＜1且m≠0 D. m≤1且m≠0

    C 【解析】试题解析：根据题意得m≠0且△=22﹣4m＞0， 所以m＜1且m≠0． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：天津市武清区2018届九年级（上）期中数学试卷 题型：填空题

    若二次函数y=x2﹣2x+m的图象与x轴有两个交点，则m的取值范围是 ．

    m＜1 【解析】 试题分析：△=0?抛物线与x轴只有一个交点，△＞0?抛物线与x轴有两个交点，△＜0?抛物线与x轴没有交点.∵二次函数y=x2﹣2x+m的图象与x轴有两个交点，∴△＞0，∴4﹣4m＞0，∴m＜1．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年度第一学期海口市八年级数学科期末检测模拟题（普通班卷） 题型：解答题

    （1）先化简，再求值: (a+1)2-(3a2+a)÷a，其中a=-3.

    （2）已知x+y=3，xy=-2. 求(x-1)(y-1)的值.

    （1）12（2）-4 【解析】试题分析：（1）先利用完全平方公式进行展开和利用多项式除以单项式进行计算，然后再合并同类项，最后代入求出即可； （2）先进行多项式的乘法计算，再整体代入，即可求出答案． 试题解析：（1）（a+1） 2 -（3a 2 +a）÷a=a 2 +2a+1-3a-1=a 2 -a， 当a=-3时，原式=（-3） 2 -（-3）=12； （2）当x+...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年度第一学期海口市八年级数学科期末检测模拟题（普通班卷） 题型：填空题

    比较大小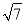： ______3.

    ＜ 【解析】∵7<9， ∴， 即<3， 故答案为：<.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年度第一学期海口市八年级数学科期末检测模拟题（普通班卷） 题型：单选题

    下列计算正确的是（ ）

    A. a3+a3=a6 B. a3·a3=a9 C. a6÷a2=a4 D. (a3)2=a5

    C 【解析】A. a3+a3=2a3 ，故A选项错误；B. a3·a3=a6 ，故B选项错误；C. a6÷a2=a4 ，正确；D. (a3)2=a6，故D选项错误， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：浙江省杭州市临安区2017-2018学年第一学期八年级数学期末综合练习数学试卷 题型：解答题

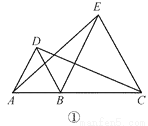
    在直线上顺次取 A，B，C 三点，分别以 AB，BC 为边长在直线的同侧作正三角形， 作得两个正三角形的另一顶点分别为 D，E．

    (1)如图①，连结 CD，AE，求证：CD＝AE；

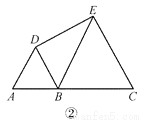
    (2)如图②，若 AB＝1，BC＝2，求 DE 的长；

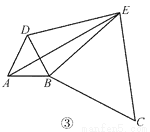
    (3)如图③，将图②中的正三角形 BCE 绕 B 点作适当的旋转，连结 AE，若有 DE2＋BE2＝ AE2，试求∠DEB 的度数．

    见解析 【解析】试题分析：（1）由△ABD和△ECB都是等边三角形可得AD=AB=BD，BC=BE=EC，∠ABD=∠EBC=60°，所以∠ABE=∠DBC，所以△ABE≌△DBC，即可证明AE=DC；（2） 如图②中，取BE中点F，连接DF，由题意不难得出BF=EF=1=BD，再结合∠DBF=60°可得△DBF是等边三角形，进而推出∠EDB=90°，再由勾股定理可求出DE的长；（3）...

    查看答案和解析>>

    科目：初中数学 来源：浙江省杭州市临安区2017-2018学年第一学期八年级数学期末综合练习数学试卷 题型：单选题

    下列判断正确的是（　　）

    A. 两边和一角对应相等的两个三角形全等 B. 一边及一锐角相等的两个直角三角形全等

    C. 顶角和底边分别相等的两个等腰三角形全等 D. 三个内角对应相等的两个三角形全等

    C 【解析】两边及其夹角对应相等的两个三角形全等，A选项错误； 若一个三角形的直角边和斜边对应相等，那么这两个三角形必然不全等，B选项错误； C选项正确； 三个内角对应相等的两个三角形相似，但是不一定全等，D选项错误. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型：单选题

    下列说法中，正确的是（ ）．

    ①在平面内，两条互相垂直的数轴，组成了平面直角坐标系；

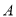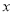    ②如果点到轴和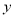轴的距离分别为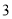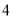， ，且点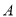在第一象限，那么；

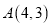    ③如果点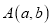位于第四象限，那么；

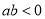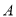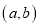    ④如果点的坐标为，那么点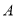到坐标原点的距离为；

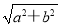    ⑤如果点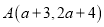在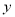轴上，那么点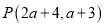的坐标是．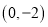

    A. ②③④ B. ②④⑤ C. ①③⑤ D. ②③⑤

    A 【解析】①在平面内，两条互相垂直且原点重合的数轴，组成了平面直角坐标系，故①错误； ②如果点到轴和轴的距离分别为， ，那么点或或或， ∵在第一象限，∴点坐标为； ③如果点位于第四象限，那么，正确； ④如果点的坐标为，那么点到坐标原点的距离为，正确； ⑤如果点在轴上，则， ∴，∴的坐标是故错误． 综上②③④正确． 故选．

    查看答案和解析>>

    同步练习册答案