
方程(x-5)( x-6)=x-5的解是( )
A. x=5 B. x=5或x=6 C. x=7 D. x=5或x=7
D 【解析】(x-5)(x-6)=x-5 (x-5)(x-6)-(x-5)=0 (x-5)(x-7)=0 解得:x1=5,x2=7; 故选D.科目:初中数学 来源:北师大版数学九年级上册第二章第三节《用公式法求解一元一次方程》课时练习 题型:解答题
解方程:x2-3x-7=0.
x1=,x2=. 【解析】试题分析:利用求根公式来解方程. 试题解析:在方程x2-3x-7=0中,a=1,b=-3,c=-7.则 x=, 解得 x1=,x2=.查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级上册第一章特殊平行四边形第二节《矩形的性质与判定》课时练习 题型:单选题
一个矩形被分成不同的4个三角形,其中绿色三角形的面积占矩形面积的15%,黄色的三角形的面积是21cm2,则该矩形的面积为( )
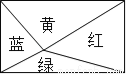
A. 60cm2 B. 70cm2 C. 120cm2 D. 140cm2
A 【解析】试题分析:黄色三角形与绿色三角形面积之和是矩形面积的50%,而绿色三角形面积占矩形面积的15%,所以黄色三角形面积占矩形面积的(50%-15%)=35%,已知黄色三角形面积是21平方厘米,故矩形的面积=21÷(50%-15%)=21÷35%=60(cm2). 故选A.查看答案和解析>>
科目:初中数学 来源:北师大版九年级数学(上)第二章《一元二次方程》同步测试:2.4用因式分解法求解一元二次方程 题型:填空题
方程x(x-2)=-(x-2)的根是_______________.
x1=2,x2=-1 【解析】【解析】 移项得:x(x﹣2)+(x﹣2)=0,∴(x﹣2)(x+1)=0,解得:x1=2,x2=﹣1.故答案为:x1=2,x2=﹣1.查看答案和解析>>
科目:初中数学 来源:北师大版九年级数学(上)第二章《一元二次方程》同步测试:2.4用因式分解法求解一元二次方程 题型:单选题
三角形两边的长是3和4,第三边的长是方程x2﹣12x+35=0的根,则该三角形的周长为( )
A. 14 B. 12 C. 12或14 D. 以上都不对
B 【解析】试题分析:解,得(x-5)(x-7)=0,∴x1=5,x2=7 又∵3,4,7不能组成三角形;∴x=5 则周长为3+4+5=12,故选B查看答案和解析>>
科目:初中数学 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:解答题
如图,点E,F分别在菱形ABCD的边DC,DA上,且CE=AF.求证:∠ABF=∠CBE.
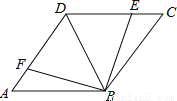
查看答案和解析>>
科目:初中数学 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:填空题
如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED= _____.
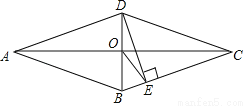
查看答案和解析>>
科目:初中数学 来源:广西柳州市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
若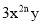 与
与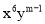 同类项,则
同类项,则 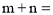 _______.
_______.
查看答案和解析>>
科目:初中数学 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:解答题
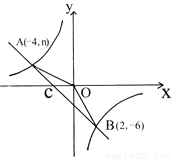
如图,已知A(-4,n)、B(2,-6)是一次函数y1=k1x+b与反比例函数y2=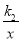 的两个交点,直线AB与x轴交于点C。
的两个交点,直线AB与x轴交于点C。
(1)求两函数解析式;(2)求△AOB的面积;
(3)根据图象回答:y1<y2时,自变量x的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com