
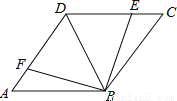
如图,点E,F分别在菱形ABCD的边DC,DA上,且CE=AF.求证:∠ABF=∠CBE.
科目:初中数学 来源:北师大版数学九年级上册第二章第三节《用公式法求解一元一次方程》课时练习 题型:填空题
写出方程x2+x-1=0的一个正根_______
【解析】【解析】 a=1,b=1,c=-1,△=1+4=5,∴x=.故正根为:x=.故答案为:x=.查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级上册第一章特殊平行四边形第二节《矩形的性质与判定》课时练习 题型:单选题
如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )
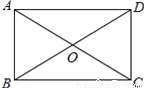
A. ∠ABC=90° B. AC=BD C. OA=OB D. OA=AD
D 【解析】试题分析:本题考查了矩形的性质;熟练掌握矩形的性质是解决问题的关键.矩形的性质:四个角都是直角,对角线互相平分且相等;由矩形的性质容易得出结论.∵四边形ABCD是矩形,∴∠ABC=∠BCD=∠CDA=∠BAD=90°,AC=BD,OA=AC,OB=BD,∴OA=OB,∴A、B、C正确,D错误查看答案和解析>>
科目:初中数学 来源:北师大版九年级数学(上)第二章《一元二次方程》同步测试:2.4用因式分解法求解一元二次方程 题型:单选题
现定义运算“★”,对于任意实数a、b,都有a★b= 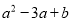 ,如:3★5=
,如:3★5=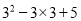 ,若x★2=6,则实数x的值是( )
,若x★2=6,则实数x的值是( )
A. 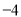 或
或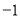 B. 4或
B. 4或 C. 4或
C. 4或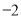 D.
D. 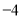 或2
或2
查看答案和解析>>
科目:初中数学 来源:北师大版九年级数学(上)第二章《一元二次方程》同步测试:2.4用因式分解法求解一元二次方程 题型:单选题
方程(x-5)( x-6)=x-5的解是( )
A. x=5 B. x=5或x=6 C. x=7 D. x=5或x=7
D 【解析】(x-5)(x-6)=x-5 (x-5)(x-6)-(x-5)=0 (x-5)(x-7)=0 解得:x1=5,x2=7; 故选D.查看答案和解析>>
科目:初中数学 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:填空题
四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE=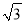 ,则CE的长为______.
,则CE的长为______.
查看答案和解析>>
科目:初中数学 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:单选题
如图,菱形ABCD的对角线AC、BD的长分别是6cm、8cm,AE⊥BC于点E,则AE的长是( )
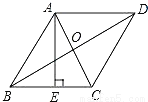
A. 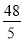 cm B.
cm B. 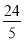 cm C.
cm C. 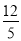 cm D.
cm D. 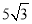 cm
cm
查看答案和解析>>
科目:初中数学 来源:广西柳州市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
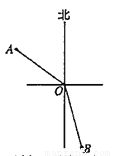
在灯塔O处观测到轮船A位于北偏西54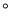 的方向,同时轮船B在南偏东15
的方向,同时轮船B在南偏东15 的方向,则∠AOB的大小为( )
的方向,则∠AOB的大小为( )
A. 69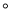 B. 111
B. 111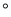 C. 159
C. 159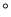 D. 141
D. 141
查看答案和解析>>
科目:初中数学 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:解答题
已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.
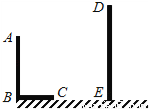
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
(1)作图见解析; (2)10m. 【解析】试题分析:(1)根据投影的定义,作出投影即可; (2)根据在同一时刻,不同物体的物高和影长成比例;构造比例关系AB:DE=BC:EF.计算可得DE=10(m). 试题解析:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影. (2)∵AC∥DF, ∴∠ACB=∠DFE. ∵∠ABC=∠DEF=...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com