
已知一次函数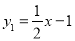 ,二次函数
,二次函数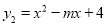 (其中m>4).
(其中m>4).
(1)求二次函数图象的顶点坐标(用含m的代数式表示);
(2)利用函数图象解决下列问题:
①若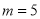 ,求当
,求当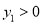 且
且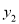 ≤0时,自变量
≤0时,自变量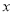 的取值范围;
的取值范围;
②如果满足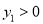 且
且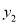 ≤0时自变量
≤0时自变量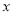 的取值范围内有且只有一个整数,直接写出
的取值范围内有且只有一个整数,直接写出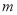 的取值范围.
的取值范围.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
解分式方程: 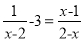
查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
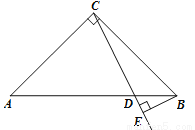
如图,已知Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上的一点(不与A、B重合).过点B作BE⊥CD,垂足为E.将线段CE绕点C顺时针旋转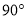 ,得到线段CF,连结EF.设∠BCE度数为
,得到线段CF,连结EF.设∠BCE度数为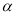 .
.
(1)①补全图形;
②试用含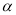 的代数式表示∠CDA.
的代数式表示∠CDA.
(2)若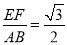 ,求
,求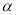 的大小.
的大小.
(3)直接写出线段AB、BE、CF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:填空题
已知∠A为锐角,且tanA=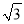 ,则∠A的大小为 _______________
,则∠A的大小为 _______________
查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:单选题
已知点A(1,m),B(2,n)在反比例函数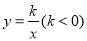 的图象上,则( )
的图象上,则( )
A. 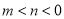 B.
B. 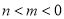 C.
C. 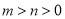 D.
D. 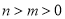
查看答案和解析>>
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:解答题
已知: 如图,⊙O的直径AB的长为5cm,C为⊙O上的一个点,∠ACB的平分线交⊙O于点D,求BD的长.

查看答案和解析>>
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:填空题
圆心角为160°的扇形的半径为9cm,则这个扇形的面积是____________cm2.
36 π . 【解析】查看答案和解析>>
科目:初中数学 来源:湖南省娄底市娄星区2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
如图,直线AB、CD相交于点O,OE平分∠AOC,∠BOC-∠BOD = 20°,求∠BOE的度数.
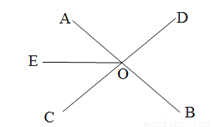
查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )
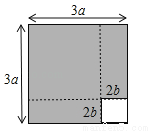
A. 3a+2b B. 3a+4b C. 6a+2b D. 6a+4b
A 【解析】【解析】 依题意有:3a﹣2b+2b×2=3a﹣2b+4b=3a+2b. 故这块矩形较长的边长为3a+2b.故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com