
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若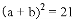 ,大正方形的面积为13,则小正方形的面积为( )
,大正方形的面积为13,则小正方形的面积为( )
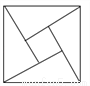
A. 3 B. 4 C. 5 D. 6
C 【解析】试题分析:如图所示,∵,∴=21,∵大正方形的面积为13,2ab=21﹣13=8,∴小正方形的面积为13﹣8=5.故选C.科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 第4章 一次函数 单元测试卷 题型:填空题
已知关于x的方程ax-5=7的解为x=1,则一次函数y=ax-12与x轴交点的坐标为________.
(1,0) 【解析】试题解析:∵x=1是关于x的方程ax-5=7的解, ∴a-5=7, 解得a=12, ∴一次函数y=ax-12可整理为y=12x-12. 令y=0,得到:12x-12=0, 解得x=1, 则一次函数图象与x轴的交点坐标是(1,0). 故答案为:(1,0).查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版16.2二次根式定义的乘除同步练习 题型:解答题
等式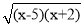 =
=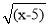 •
•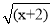 一定成立吗?
一定成立吗?
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2017-2018学年八年级上学期期中数学 题型:解答题
如图所示,在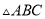 中,
中, 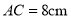 ,
, 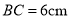 ,在
,在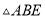 中,
中, 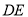 为
为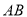 边上的高,
边上的高, 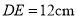 ,
, 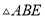 的面积
的面积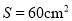 .
.
(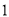 )求出
)求出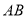 边的长.
边的长.
(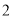 )你能求出
)你能求出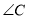 的度数吗?请试一试.
的度数吗?请试一试.

查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2017-2018学年八年级上学期期中数学 题型:填空题
命题“等腰三角形的两腰上的高线相等” 的逆命题是:_______________________.
两边上高线相等的三角形是等腰三角形 【解析】【解析】 命题“等腰三角形两腰上的高相等”的逆命题是:两边上高线相等的三角形是等腰三角形. 故答案为:两边上高线相等的三角形是等腰三角形.查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2017-2018学年八年级上学期期中数学 题型:单选题
下面四个手机应用软件图标中是轴对称图形的是 ( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第三章圆单元检测卷 题型:填空题
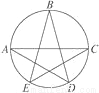
如图,已知A、B、C、D、E均在⊙O上,且AC为⊙O的直径,则∠A+∠B+∠C=________度.
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第三章圆单元检测卷 题型:单选题
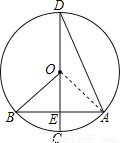
如图,已知圆O的直径为6,CD为圆O的直径,且CD⊥AB,∠D=15°.则OE的长为( )
A. 3 B. 3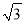 C.
C. 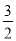 D.
D. 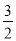
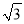
查看答案和解析>>
科目:初中数学 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
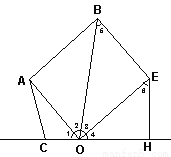
如图,BE∥AO,∠1=∠2,OE⊥OA于点O,EH⊥CO于点H,那么∠5=∠6,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com