
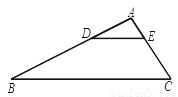
如图,在△ABC中,点D,E分别为边AB,AC上的点,且DE∥BC,若AD=4,BD=8,AE=2,则CE的长为 ( )
A. 2 B. 4 C. 6 D. 8
B 【解析】∵在△ABC中,点D,E分别为边AB,AC上的点,DE∥BC, ∴, 又∵AD=4,BD=8,AE=2, ∴, ∴ 4EC=16, ∴EC=4. 故选B. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:内蒙古赤峰市宁城县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
计算:
(1)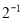 +|﹣
+|﹣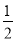 |+(
|+(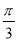 )0
)0
(2)已知:a﹢b=4,ab = 3,求:a2﹢b2的值。
(1)2;(2)10. 【解析】试题分析:(1)先乘方,化简绝对值,再加减计算,(2)先将a+b=4,两边同时平方,再移项可求出a2﹢b2. 试题解析:(1)+|﹣|+()0, 原式=, (2) ∵ a﹢b=4,ab = 3, ∴ a2﹢b2=(a﹢b)2﹣2ab=42﹣2×3=10.查看答案和解析>>
科目:初中数学 来源:辽宁省2018届九年级(上)期末模拟数学试卷 题型:单选题
用配方法解一元二次方程ax2+bx+c=0(a≠0),此方程可变形为( )
A. 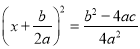 B.
B. 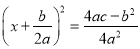
C. 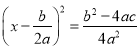 D.
D. 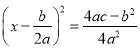
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期初三数学期末试卷 题型:填空题
阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:△OAB.
求作:⊙O,使⊙O与△OAB的边AB相切.

小明的作法如下:
如图,①取线段OB的中点M;以M为圆心,MO为半径作⊙M,与边AB交于点C;
②以O为圆心,OC为半径作⊙O;
所以,⊙O就是所求作的圆.
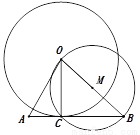
请回答:这样做的依据是__________________________________________________.
圆的定义,直径的定义,直径所对的圆周角为90°,到线段两端点距离相等的点在线段的垂直平分线上,经过半径的外端并且垂直于这条半径的直线是圆的切线. 【解析】∵要作出线段OB的中点M, ∴需作线段OB的垂直平分线,交OB于点M, ∴OM=MB(线段垂直平分线上的点到线段两端的距离相等); ∵以M为圆心,MO为半径作⊙M(圆的定义), ∴OB是⊙M的直径(直径定义), ...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期初三数学期末试卷 题型:填空题
分解因式:3x3-6x2+3x=_________.
3x(x-1)2 【解析】. 故答案为: .查看答案和解析>>
科目:初中数学 来源:江苏省南通市崇川区2015-2016学年八年级上学期期末考试数学试卷 题型:解答题
选取二次三项式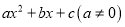 中的两项,配成完全平方式的过程叫配方.
中的两项,配成完全平方式的过程叫配方.
例如:①选取二次项和一次项配方: 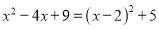 ;
;
②选取二次项和常数项配方: 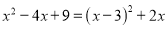 ,或
,或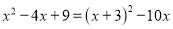
③选取一次项和常数项配方: 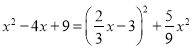
根据上述材料,解决下面问题:
(1)写出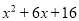 的两种不同形式的配方;
的两种不同形式的配方;
(2)已知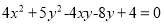 ,求
,求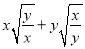 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:江苏省南通市崇川区2015-2016学年八年级上学期期末考试数学试卷 题型:解答题
因式分解:
(1) 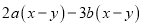 (2)
(2)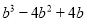
查看答案和解析>>
科目:初中数学 来源:江苏省南通市崇川区2015-2016学年八年级上学期期末考试数学试卷 题型:单选题
下列式子是分式的是
A. 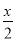 B.
B. 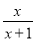 C.
C. 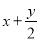 D.
D. 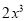
查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年七年级(上)期末模拟数学试卷 题型:填空题
一位美术老师在课堂上进行立体模型素描教学时,把14个棱长为1分米的正方体摆在课桌上成如图形式,然后他把露出的表面都涂上不同的颜色,则被他涂上颜色部分的面积为_________平方分米.
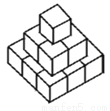
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com