
�ı���ABCD�ڽ��ڡ�O����EΪAD��һ�㣬����AC��CB����B=��AEC��
��1����ͼ1����֤��CE=CD��
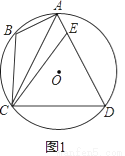
��2����ͼ2������B+��CAE=120�㣬��ACD=2��BAC�����BAD�Ķ�����
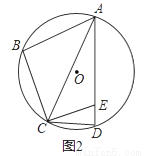
��3����ͼ3���ڣ�2���������£��ӳ�CE����O�ڵ�G����tan��BAC= 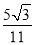 ��EG=2����AE�ij���
��EG=2����AE�ij���
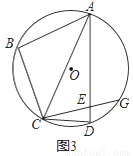
���𰸡���1������������2��60�㣻��3��7.
�����������������(1)����Բ���ڽ��ı��ζ����õ���CED=��CDE.
(2) ��CH��DE��H, ���ECH=�����ɣ�1��CE=CD���æ���ʾ��CAE����BAC������BAD=��BAC+��CAE.��3������AG����GN��AC��AM��EG����֤����CAG=��BAC����NG=5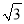 m���ɵ�AN=11m������ֱ��
m���ɵ�AN=11m������ֱ�� AGM,
AGM,  AEM�����ɶ����������m��ֵ�����AE��.
AEM�����ɶ����������m��ֵ�����AE��.
���������
��1����������
֤�������ı���ABCD�ڽ��ڡ�O.
���B+��D=180�㣬
�ߡ�B=��AEC��
���AEC+��D=180�㣬
�ߡ�AEC+��CED=180�㣬
���D=��CED��
��CE=CD��
��2����������
��CH��DE��H��
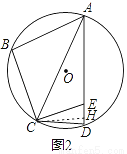
���ECH=�����ɣ�1��CE=CD��
���ECD=2����
�ߡ�B=��AEC����B+��CAE=120�㣬
���CAE+��AEC=120�㣬
���ACE=180�㩁��AEC����ACE=60�㣬
���CAE=90�㩁��ACH=90�㩁��60��+����=30�㩁����
��ACD=��ACH+��HCD=60��+2����
�ߡ�ACD=2��BAC��
���BAC=30��+����
���BAD=��BAC+��CAE=30��+��+30�㩁��=60�㣮
��3����������
����AG����GN��AC��AM��EG��
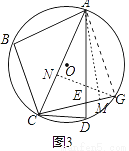
�ߡ�CED=��AEG����CDE=��AGE����CED=��CDE��
���AEG=��AGE��
��AE=AG��
��EM=MG=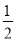 EG=1��
EG=1��
���EAG=��ECD=2����
���CAG=��CAD+��DAG=30�㩁��+2��=��BAC��
��tan��BAC=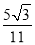 ��
��
����NG=5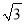 m���ɵ�AN=11m��AG=
m���ɵ�AN=11m��AG=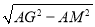 =14m��
=14m��
�ߡ�ACG=60�㣬
��CN=5m��AM=8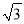 m��MG=
m��MG=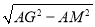 =2m=1��
=2m=1��
��m=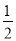 ��
��
��CE=CD=CG��EG=10m��2=3��
��AE=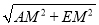 =
=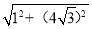 =7��
=7��
�����͡������
��������
27
���κ���y=��x��1��2+k�ֱ���x�ᡢy�ύ��A��B��C���㣬��A�ڵ�B����ֱ࣬��y=��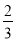 x+2������B������y�ύ�ڵ�D��
x+2������B������y�ύ�ڵ�D��
��1����ͼ1����k��ֵ��
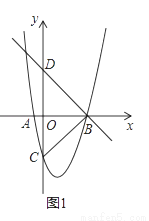
��2����ͼ2���ڵ�һ��������������һ����P������AP����P��PE��x���ڵ�E����E��EF��AP�ڵ�F������D��ƽ����x���ֱ�߷ֱ���ֱ��FE��PE���ڵ�G��H�����P�ĺ�����Ϊt���߶�GH�ij�Ϊd����d��t�ĺ�����ϵʽ����ֱ��д��t��ȡֵ��Χ��
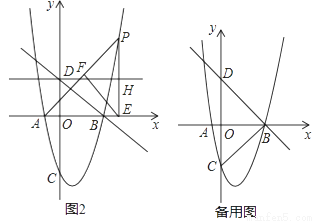
��3���ڣ�2���������£�����G��ƽ����y���ֱ�߷ֱ�AP��x����������ڵ�M��T��N��tan��MEA= 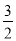 ����KΪ����������������һ�㣬���ڶԳ�����࣬����KA��������KA��ȡһ��R������RM������K��KQ��AK��PE���ӳ�����Q������AQ��HK������RAE����RMA=45�㣬��AKQ���HKQ�������ȣ����R�����꣮
����KΪ����������������һ�㣬���ڶԳ�����࣬����KA��������KA��ȡһ��R������RM������K��KQ��AK��PE���ӳ�����Q������AQ��HK������RAE����RMA=45�㣬��AKQ���HKQ�������ȣ����R�����꣮

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ������ʡ���꼶���£��ڶ��β�����ѧ�Ծ� ���ͣ���ѡ��
һ���̵꽫ij�ַ�װ���ɱ������40%��ۣ�����8���Ż����������ÿ����װ�Կɻ���15Ԫ�������ַ�װÿ���ijɱ����ǣ�������
A. 140Ԫ B. 135Ԫ C. 125Ԫ D. 120Ԫ
C �������������ַ�װÿ���ijɱ���ΪxԪ�����ݱ��-�ɱ�=���ɵã�80%����1+40%��x��x=15����ã�x=125�����ַ�װÿ���ijɱ�Ϊ125Ԫ�� ��ѡ��C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ16-17ѧ��ȵ�һѧ�����꼶��ѧ��ĩ���Ծ� ���ͣ���ѡ��
���и�ͼ���У������۵���Χ��һ����������ǣ� ��

A. A B. B C. C D. D
A ���������������չ��ͼ�в��ܳ��֡��������Σ��������κ͡�����Σ���ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ũҵ��ѧ������ѧ2017-2018ѧ����꼶��ѧ�ڵ������¿���ѧ�Ծ� ���ͣ������
���㣺 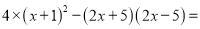 _________.
_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ũҵ��ѧ������ѧ2017-2018ѧ����꼶��ѧ�ڵ������¿���ѧ�Ծ� ���ͣ���ѡ��
��֪x2+kxy+64y2��һ����ȫʽ����k��ֵ�ǣ�������
A. 8 B. ��8 C. 16 D. ��16
D ���������������� ��x2+kxy+16y2��һ����ȫƽ��ʽ�� ���2��x��4y=kxy�� ��k=��8�� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ���������㷻��2017���п���ѧ��ģ�Ծ��������棩 ���ͣ������
�Ȼ�������ֵ�� 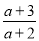 �£�
�£�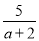 -a+2��������a=2sin60��+3tan45�㣮
-a+2��������a=2sin60��+3tan45�㣮
���𰸡���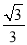 .
.
���������������������ʽ�ֽ⣬��ͨ�֣�Լ�ֻ�������ֵ��ֵ.
���������
��������
ԭʽ= 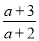 �£�
�£�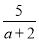 -
-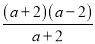 ��
��
=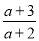 ��
��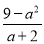 =
=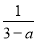 ��
��
��a=2sin60��+3tan45��=2��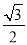 +3��1=
+3��1=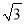 +3
+3
��ԭʽ=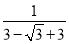 =��
=��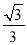 .
.
�㾦��������ʽ���ʽ����
��ʽ����ʽA������ʽB,���Ա�ʾ�ɵ�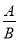 ����ʽ.���B�к�����ĸ,��ô��
����ʽ.���B�к�����ĸ,��ô�� 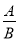 Ϊ��ʽ.��ʽ�ص���û�еȺţ���ʽ�Ӽ�һ����Ҫͨ��.
Ϊ��ʽ.��ʽ�ص���û�еȺţ���ʽ�Ӽ�һ����Ҫͨ��.
��2����ʽ���̣���ĸ�к���δ֪���ķ��̽�����ʽ����.�ص����еȺţ�Ҫ��ȷ�����ĸ��ȥ��ĸ��ʱ��Ҫÿһ��������ĸ������һ�㲻��Ҫͨ�֣�����Ҫ����.
�����͡������
��������
22
ͼ1��ͼ2��������״�ʹ�С��ȫ��ͬ�ķ���ֽ������ֽ��ÿ��С�����εı߳���Ϊ1���߶�AB�������˵����С�����εĶ����ϣ�
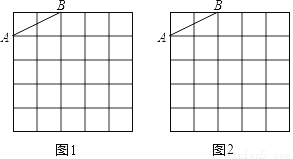
��1����ͼ1����С�����εĶ�����ȷ��һ��C������AC��BC��ʹ�á�ABCΪֱ�������Σ������Ϊ5����ֱ��д����ABC���ܳ���
��2����ͼ2����С�����εĶ�����ȷ��һ��D������AD��BD��ʹ�á�ABD����һ���ڽ�Ϊ45�㣬�����Ϊ3��
��1��5+3;��2��3. �������������������1������ֱ�������Σ�AB=����ֱ�DZ�,�����5�������������һ��ֱ�DZ�BC���ȣ��������AC. (2)�ȹ���һ��45��ǣ������������3���ɻ���ͼ��. ��������� ��1���������� ��ͼ1��ʾ����ABC��Ϊ���� ��ABC���ܳ�Ϊ�� +2+5=5+3�� ��2���������� ��ͼ2��ʾ����ABD�У���ADB=45�㣬����...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ���������㷻��2017���п���ѧ��ģ�Ծ��������棩 ���ͣ������
��ʽ�֡�������
xy2��x2y=________��
���𰸡�xy��y��x��
��������xy2��x2y=xy(y-x).
�ʴ�Ϊxy(y-x).
�����͡������
��������
15
������y=3��x��2��2+5�Ķ��������� ��
��2��5���� ���������������������������y=a��x��h��2+k�Ķ�������Ϊ��h��k�����ɴ˼�����⣮ �������� ��������y=3��x��2��2+5�� �ඥ������Ϊ����2��5���� �ʴ�Ϊ����2��5�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018����ѧ�ھ��꼶��ѧ��ĩ�Ծ� ���ͣ������
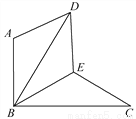
��ͼ����BAD���ɡ�BEC��ƽ�����Ƶ�B��ת60����ã���AB��BC��BE��CE������DE.
��1����֤����BDE�ա�BCE��
��2�����ж��ı���ABED����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2018ѧ������꼶���ϣ���ѧ��ĩ���Ծ� ���ͣ���ѡ��
��ͼ���ĸ��������������ϵĶ�Ӧ��M��P��N��Q������M��N��ʾ����������Ϊ�෴������ͼ�б�ʾ����ֵ��С�����ĵ��ǣ�������
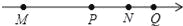
A. ��M B. ��N C. ��P D. ��Q
C ������������������ߵ�M��N��ʾ����������Ϊ�෴������ԭ���λ�ô�Լ��O�㣬 �����ֵ��С�����ĵ���P�㣬��ѡC���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com