
如图,在⊙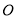 的内接四边形
的内接四边形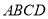 中,
中, 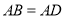 ,
, 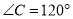 ,点
,点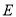 在弧
在弧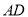 上.若
上.若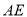 恰好为⊙
恰好为⊙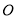 的内接正十边形的一边,弧
的内接正十边形的一边,弧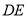 的度数为__________.
的度数为__________.

科目:初中数学 来源:黄金30题系列 八年级数学 大题好拿分 题型:解答题
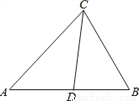
已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.
查看答案和解析>>
科目:初中数学 来源:湖南省衡阳市2018届九年级上期末模拟数学试卷 题型:解答题
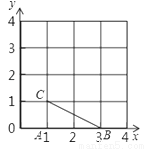
如图,在直角坐标系中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点).
(1)在第一象限内找一点P,以格点P、A、B为顶点的三角形与△ABC相似但不全等,请写出符合条件格点P的坐标;
(2)请用直尺与圆规在第一象限内找到两个点M、N,使∠AMB=∠ANB=∠ACB.请保留作图痕迹,不要求写画法.
查看答案和解析>>
科目:初中数学 来源:湖南省衡阳市2018届九年级上期末模拟数学试卷 题型:单选题
下列方程中,关于x的一元二次方程是( )
A. 3(x+1)2=2(x+1) B. 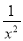 +
+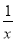 -2=0
-2=0
C. ax2+bx+c=0 D. x2+2x=x2-1
A 【解析】【解析】 A是二元二次方程,故A错误; B是分式方程,故B错误; 当a=0时C不是一元二次方程,故C错误; D是一元二次方程. 故选D.查看答案和解析>>
科目:初中数学 来源:浙江杭州上城区北师大附属杭州中学2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
已知抛物线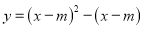 ,其中
,其中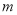 是常数,该抛物线的对称轴为直线
是常数,该抛物线的对称轴为直线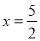 .
.
(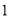 )求该抛物线的函数解析式.
)求该抛物线的函数解析式.
(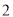 )把该抛物线沿
)把该抛物线沿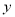 轴向上平移多少个单位后,得到的抛物线与
轴向上平移多少个单位后,得到的抛物线与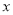 轴只有一个公共点.
轴只有一个公共点.
查看答案和解析>>
科目:初中数学 来源:浙江杭州上城区北师大附属杭州中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
如图,在⊙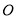 ,
, 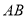 为直径,点
为直径,点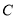 为圆上一点,将劣弧
为圆上一点,将劣弧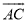 沿弦
沿弦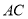 翻折交
翻折交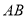 于点
于点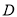 ,连接
,连接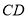 ,如果
,如果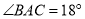 ,则
,则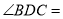 ( ).
( ).

A. 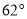 B.
B. 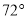 C.
C. 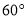 D.
D. 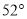
查看答案和解析>>
科目:初中数学 来源:浙江杭州上城区北师大附属杭州中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
已知线段a=2,b=4,则线段a,b的比例中项为( )
A.3 B.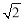 C.
C.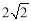 D.
D.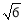
查看答案和解析>>
科目:初中数学 来源:重庆市2017年中考数学二模试卷 题型:单选题
如图,小桥用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第8个图案中共有( )和黑子.
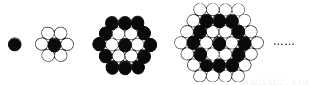
A. 37 B. 42 C. 73 D. 121
C 【解析】【解析】 第1、2图案中黑子有1个,第3、4图案中黑子有1+2×6=13个,第5、6图案中黑子有1+2×6+4×6=37个,第7、8图案中黑子有1+2×6+4×6+6×6=73个.故选C.查看答案和解析>>
科目:初中数学 来源:2017年重庆市中考数学模拟试卷 题型:解答题
x2﹣4x+1=0(用配方法)
x1=2+,x2=2﹣. 【解析】试题分析:先移项,然后配方,解出x即可. 试题解析:x2-4x+1=0, 移项,得x2-4x=-1, 配方,得x2-4x+4=-1+4,即(x-2)2=3, 解得,x-2=, 即x1=2+,x2=2-.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com