
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:单选题
因式分【解析】
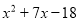 的结果为( )
的结果为( )
A. 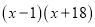 B.
B. 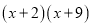 C.
C. 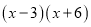 D.
D. 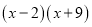
查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:单选题
如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( )
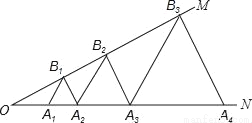
A. 6 B. 12 C. 32 D. 64
C 【解析】试题分析:;……,则,即△的边长为64.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.求证:AD=BC.
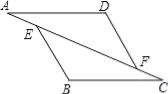
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:填空题
已知: 如图, AC、BD相交于点O, ∠A =∠D, 请你再补充一个条件,使△AOB ≌△DOC你补充的条件是 __________________________.

查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:单选题
若关于x的方程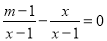 有增根,则m的值是( )
有增根,则m的值是( )
A. 2 B. 1 C. 0 D. -1
A 【解析】方程两边都乘(x?1),得m?1?x=0, ∵方程有增根, ∴最简公分母x?1=0,即增根是x=1, 把x=1代入整式方程,得m=2. 故选:A.查看答案和解析>>
科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
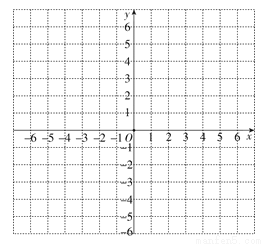
在平面直角坐标系中,将某点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这个点的“互换点”,如(-3,5)与(5,-3)是一对“互换点”.
(1)以O为圆心,半径为5的圆上有无数对“互换点”,请写出一对符合条件的“互换点”;
(2)点M,N是一对“互换点”,点M的坐标为(m,n),且(m>n),⊙P经过点M,N.
①点M的坐标为(4,0),求圆心P所在直线的表达式;
②⊙P的半径为5,求m-n的取值范围.
查看答案和解析>>
科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:填空题
请写出一个过点(1,1),且与x轴无交点的函数表达式________________.
答案不唯一,如: 【解析】试题分析:首先与x轴无交点,则考虑反比例函数和开口向上且顶点在一、二象限的二次函数。然后设出解析式,把(1,1)带入即可求得解析式.查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:填空题
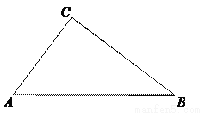
如图,已知在Rt△ABC中,∠ACB=90°,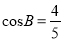 ,BC=8,点D在边BC上,将△ABC沿着过点D的一条直线翻折,使点B落在AB边上的点E处,联结CE、DE,当∠BDE=∠AEC时,则BE的长是 .
,BC=8,点D在边BC上,将△ABC沿着过点D的一条直线翻折,使点B落在AB边上的点E处,联结CE、DE,当∠BDE=∠AEC时,则BE的长是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com