练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

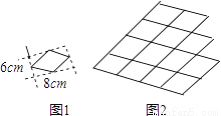
    如图，要拼出和图中的菱形相似的较长对角线为88cm的大菱形（如图）需要图1中的菱形的个数为________.

    121 【解析】小菱形的对角线长为8，大菱形的对角线长为88，相似比为8：88=1：11， 设小菱形的面积为单位1，则大菱形的面积为112=121个单位， 菱形的个数为121， 故答案为：121.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版七年级下册 第1-3章 综合测试卷 题型：填空题

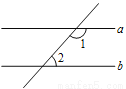
    如图，已知直线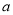∥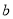，∠1＝120°，则∠2的度数是 ．

    60° 【解析】试题分析：∵直线∥， ∴∠1+∠2=180°，（两直线平行，同旁内角互补） ∵∠1＝120° ∴∠2=180°－∠1=180°－120°=60°.

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学全册综合测试卷 题型：单选题

    如图，由∠1=∠2，∠D=∠B，推出以下结论，其中错误的是（ ）

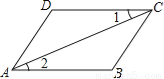
    A. AB∥DC B. AD∥BC C. ∠DAB=∠BCD D. ∠DCA=∠DAC

    D 【解析】【解析】 ∵∠1=∠2， ∴AB∥DC，故A选项结论正确； ∴∠D+∠BAD=180°，∠B+∠BCD=90°， ∵∠D=∠B， ∴∠B+∠BAD=180°，∠DAB=∠BCD，故C选项结论正确； ∴AD∥BC，故B选项结论正确； 只有AC平分∠BAD时，∠DCA=∠DAC，故D选项结论错误． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年度九年级（上）数学第一次月考试卷（11月份）(解析版) 题型：解答题

    如图，AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为AB边上一动点，若△PAD与△PBC是相似三角形，求AP的长．

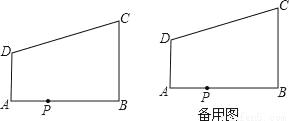
    AP=或AP=2或AP=6 【解析】试题分析:由AD//BC, ∠B=90°,可证∠PAD=∠PBC=90°, 又由AB=8,AD=3,BC=4,设AP的长为x,则BP长为8-x,然后分别从APD∽△BPC与△APD∽△BCP去分析,利用相似三角形的对应边成比例求解即可求得答案. 试题解析:∵ AB⊥BC, ∴ ∠B=90°, ∵ AD∥BC, ∴ ∠A=180°﹣∠...

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年度九年级（上）数学第一次月考试卷（11月份）(解析版) 题型：填空题

    已知Rt△ABC中，∠ACB=90°，AC=6，BC=8，点D是AB中点，点E是直线AC上一点，若以C、D、E为顶点的三角形与△ABC相似，则AE的长度为_____．

    3或 【解析】∵∠ACB=90°,AC=6,BC=8, ∴AB=62+82=10, ∵点D是AB中点, ∴CD=5, ∵CD=AD, ∴∠A=∠ACD, ∴C,D,E为顶点的三角形与△ABC相似，应分△ABC∽△CDE和△ABC∽△CED两种情况进行讨论: 当△ABC∽△CDE时: , 则,即CE=3,得到:AE=3, 当△ABC∽△CE...

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年度九年级（上）数学第一次月考试卷（11月份）(解析版) 题型：单选题

    如图所示是两根标志杆在地面上的影子，根据这些地面上的投影，你能判断出在灯光下的影子的是（　　）

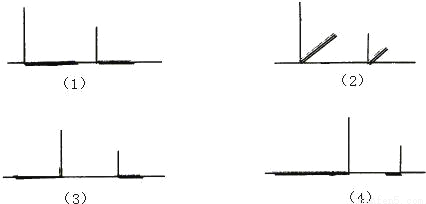
    A. （1）和（2） B. （2）和（3） C. （2）和（4） D. （3）和（4）

    D 【解析】根据物体的顶端和影子顶端的连线必经过光源可得图中连接物的顶端与影子的顶端的两条直线应有交点,故只有(3)(4)符合题意,故选D.

    查看答案和解析>>

    科目：初中数学 来源：2018届九年级中考数学专题复习同步练习题：平行四边形 题型：解答题

    已知AC是菱形ABCD的对角线，∠BAC＝60°，点E是直线BC上的一个动点，连接AE，以AE为边作菱形AEFG，并且使∠EAG＝60°，连接CG，当点E在线段BC上时，如图1，易证：AB＝CG＋CE.

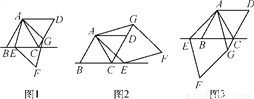
    (1)当点E在线段BC的延长线上时(如图2)，猜想AB，CG，CE之间的关系并证明；

    (2)当点E在线段CB的延长线上时(如图3)，直接写出AB，CG，CE之间的关系．

    (1)AB＝CG－CE(2)AB＝CE－CG 【解析】试题分析：（1）根据菱形的性质可得AC=AD，AE=AG，然后证明∠DAG=∠CAE，可利用SAS证明△ACE≌△ADG，根据全等三角形的性质可得CE=DG，再根据线段的和差关系和等量代换可得答案； （2）方法与（1）类似可证明△ACG≌△ABE，进而得到BE=CG，然后可得AB=CE﹣CG． 试题解析：(1)AB=CG-CE...

    查看答案和解析>>

    科目：初中数学 来源：2018届九年级中考数学专题复习同步练习题：平行四边形 题型：单选题

    如图，在Rt△ABC中，∠A＝30°，BC＝1，点D，E分别是直角边BC，AC的中点，则DE的长为(　　)

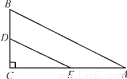
    A. 1 B. 2 C. 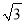D. 1＋

    A 【解析】如图,∵在Rt△ABC中,∠C=90°,∠A=30°， ∴AB=2BC=2. 又∵点D.E分别是AC、BC的中点， ∴DE是△ACB的中位线， ∴DE=AB=1. 故选：A.

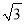
    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学 第三章 图形的平移与旋转 单元检测卷 题型：填空题

    如图，P是等边三角形ABC中的一个点，PA=2，PB=2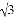， PC=4，则三角形ABC的边长为________ 

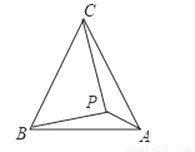
    2 【解析】试题分析：将△BAP绕B点逆时针旋转60°得△BCM，则BA与BC重合，如图， ∴BM＝BP，MC＝PA＝2，∠PBM＝60°． ∴△BPM是等边三角形， ∴PM＝PB＝， 在△MCP中，PC＝4， ∴PC2＝PM2＋MC2且PC＝2MC． ∴△PCM是直角三角形，且∠CMP＝90°，∠CPM＝30°． 又∵△PBM是等边三角形，∠BPM...

    查看答案和解析>>

    同步练习册答案