
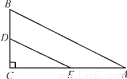
如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为( )
A. 1 B. 2 C. 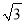 D. 1+
D. 1+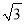
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:填空题
如果不等式3x﹣m≤0的正整数解是1,2,3,那么m的范围是________.
9≤m<12 【解析】解不等式3x﹣m≤0,得:x≤, 因为正整数解为1,2,3, 所以:3≤<4, 所以:9≤m<12 , 故答案为:9≤m<12 .查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:填空题
如图,要拼出和图中的菱形相似的较长对角线为88cm的大菱形(如图)需要图1中的菱形的个数为________.
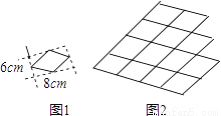
查看答案和解析>>
科目:初中数学 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:填空题
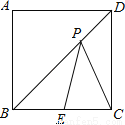
如图,正方形ABCD的边长为2,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是 .
查看答案和解析>>
科目:初中数学 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:单选题
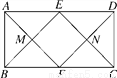
如图,在矩形ABCD中,AD=2AB,点E,F分别是AD,BC的中点,连接AF与BE,CE与DF分别交于点M,N两点,则四边形EMFN是( )
A. 正方形 B. 菱形 C. 矩形 D. 无法确定
A 【解析】∵四边形ABCD为矩形, ∴AD∥BC,AD=BC, 又∵E,F分别为AD,BC中点, ∴AE∥BF,AE=BF,ED∥CF,DE=CF, ∴四边形ABFE为平行四边形,四边形BFDE为平行四边形, ∴BE∥FD,即ME∥FN, 同理可证EN∥MF, ∴四边形EMFN为平行四边形, ∵四边形ABFE为平行四边形,∠ABC为直角, ...查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
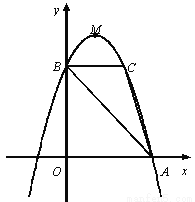
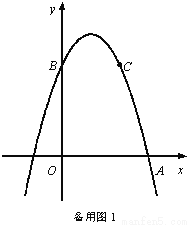
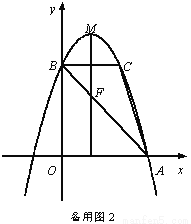
如图,抛物线y=ax 2+bx+c的顶点为M(1,4),与x轴的右交点为A,与y轴的交点为B,点C与点B关于抛物线的对称轴对称,且S△ABC =3.
(1)求抛物线的解析式;
(2)点D是y轴上一点,将点D绕C点逆时针旋转90°得到点E,若点E恰好落在抛物线上,请直接写出点D的坐标;
(3)设抛物线的对称轴与直线AB交于点F,问:在x轴上是否存在点P,使得以P、A、F为顶点的三角形与△ABC相似?若存在,求点P的坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
(1)解不等式:2+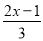 ≤x ; (2)解方程:x2-4x-1=0;
≤x ; (2)解方程:x2-4x-1=0;
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:单选题
下列选项中,与xy2是同类项的是( )
A. x2y2 B. 2x2y C. xy D. ﹣2xy2
D 【解析】A选项:x2y2与xy2相同字母的指数不同,不是同类项,故本选项错误; B、2x2y与xy2相同字母的指数不同,不是同类项,故本选项错误; C、xy与xy2相同字母的指数不同,不是同类项,故本选项错误; D、-2xy2与xy2相同字母的指数相同,是同类项,故本选项正确; 故选D.查看答案和解析>>
科目:初中数学 来源:北师大版七年级上册数学全册综合测试卷 题型:单选题
某超市进了一批商品,每件进价为a元,若要获利25%,则每件商品的零售价应定为( )
A. 25%a元 B. (1-25%)a元 C. (1+25%)a元 D.  元
元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com